How do you find the area using the trapezoid approximation method, given #1/x^2 dx #, on the interval [1,3] with n=5?
1 Answer
May 21, 2017
Trapezium rule gives:
# int_1^3 \ 1/x^2 \ dx ~~ 0.69 # (2dp)
Explanation:
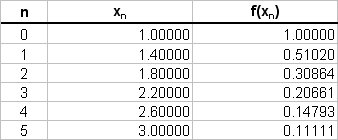
The values of
Using the trapezoidal rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
We have:
# int_1^3 \ 1/x^2 \ dx #
# " " ~~ 0.4/2 { 1 + 0.11111 + 2(0.5102 + 0.30864 + 0.20661 + 0.14793) } #
# " " = 0.2 { 1.11111 + 2(1.17339) } #
# " " = 0.2 { 1.11111 + 2.34677 } #
# " " = 0.2 * 3.45788 #
# " " = 0.69158 #
Let's compare this to the exact value:
# int_1^3 \ 1/x \ dx = [-1/x]_1^3 #
# " " = (-1/3) - (-1) #
# " " = 2/3 #