Question

A cone has a height of `8 cm` and its base has a radius of `6 cm`. If the cone is horizontally cut into two segments `7 cm` from the base, what would the surface area of the bottom segment be?

Answer 1

Area is `765/8pi` `cm^2~~300.42` `cm^2`

Explanation:

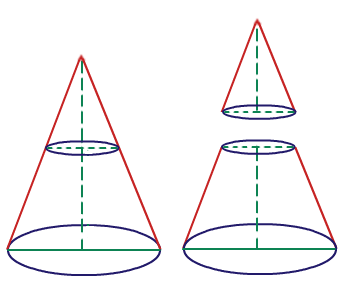Figure 1

So we have a cone that has been sliced into 2. The bottom cone consists of two circles and a frustum. The flattened frustum can be seen on the right side of the image below.

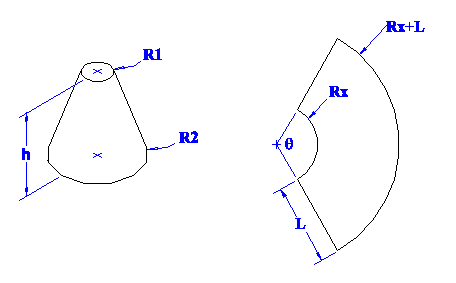Figure 2

We can see that the area of the frustum is just the difference between the area difference of the sector 2 concentric circles.
This area difference is essentially the formula for the area of a frustum:
`A=pi(R+r)sqrt((R-r)^2+h^2)`

Ignoring Figure 2 and its labels, `R` here is the big circle's radius and `r` is the smaller circle's radius, and `h` is the height of the frustum.

Back to Figure 1, the height `h` of the bottom portion of the cone is `7cm` as stated in the problem, and the radius `R` of the bottom is `6cm`. Now we just need to find `r`.

Recall `tantheta=(opposite)/(adjacent)`

In the cone, image `2theta` as the angle at the vertex of the cone (refer to Figure 1). In that case, the opposite side would be the radius of the cone, `R` and the adjacent side would be the height of the cone, `h`.

`tantheta=R/h=6/8=3/4`

However, the opposite side of `theta` can also be `r`, the radius of the top of the frustum and the adjacent side can also be `h-7cm` or `1`. In this case:

`tantheta=r/(h-7)=r`

Substitute `tantheta=3/4`:
`r=3/4`

Phew!

Now, we can finally calculate the area of the frustum! `A=pi(R+r)sqrt((R-r)^2+h^2)`
where `R=6cm`, `h=7cm`, `r=3/4cm`
`A=(945)/(16)pi` `cm^2`

Now we can calculate the areas of the top and bottom circles easily and add it all together:

`A_("total")=945/16pi+9/16pi+36pi`
`=pi(945/16+9/16+36)`
`=765/8pi` `cm^2`
`~~300.42` `cm^2`

`:.` The surface area of the bottom portion is around `300.42` `cm^2`