Question

How do you use log tables to find logarithm and the antilogarithm of `445.66` ?

Answer 1

`log 445.66 ~~ 2.6490`

`10^445.66 ~~ 4.571 xx 10^445`

Explanation:

`color(white)()`
Log of `445.66`

In the log table, find the row for numbers beginning `44` and examine the columns for `5` and `6`.

They will contain numbers like `6484` and `6493` respectively.

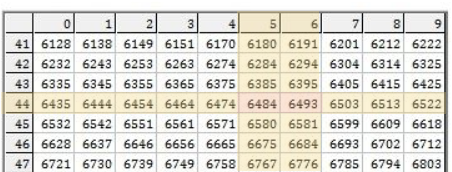
Then since `445.66` is about `2/3` of the way between `445` and `446`, we add `(6493-6484)*2/3 = 6` to `6484` to get `6490`

Hence the logarithm of `4.4566` is approximately `0.6490`

Then:

`log(445.66) = log(100*4.4566)`

`= log(100)+log(4.4566) ~~ 2+0.6490 = 2.6490`

`color(white)()`
Antilog of `445.66`

In the antilog table against `0.66` in the `0` column, we find something like `4571`

That tells us that `10^0.66 ~~ 4.571`

Hence:

`10^445.66 ~~ 4.571 xx 10^445`