How will you answer this?
A particle moving in a straight line has a velocity of v" " ms^-1 such that, t seconds after leaving a fixed point, v = 4t^2 - 8t + 3 .
Find the total distance the particle has travelled when t=1.5.
A particle moving in a straight line has a velocity of
Find the total distance the particle has travelled when t=1.5.
1 Answer
May 27, 2017
Explanation:
Observing the
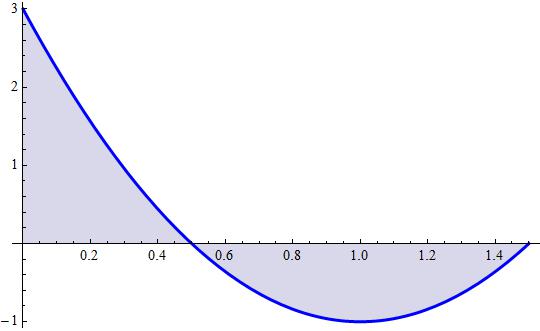
we know that the area represents the distance. In the graphics, the positive area and the negative area are equal so the movement is a movement that returns to the initial position after having attained a distance
Now equating

