Two charges of # 3 C # and # -1 C# are positioned on a line at points # 6 # and # 5 #, respectively. What is the net force on a charge of # 2 C# at # -2 #?
1 Answer
May 31, 2017
Explanation:
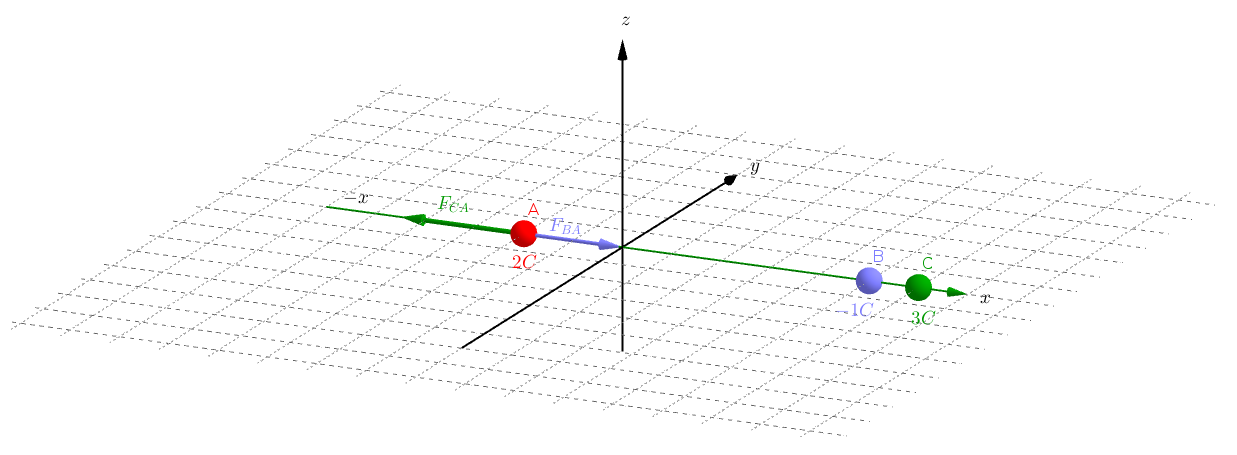
- The position of the point electric charges in the symbolic figure above is exaggerated.
- Coulomb's law states that electrical charges will force each other.
- It is a force pushing or pulling force between two charges.
- If the charges are the same, pushing is made, if it is reversed, pulling force occurs.
- We can calculate the force that the electric charges apply to each other by using the formula given below.
- Both the B and C spheres apply force to the A sphere.
- The net force applied to A is equal to the vector sum of the forces.
- Let's calculate the force that B applies to A.
- Let's calculate the force that C applies to A.
- Now let's find the vector sum.
- The net force is in negative x direction.

