Question

A triangle has vertices A, B, and C. Vertex A has an angle of `pi/12`, vertex B has an angle of `(5pi)/12`, and the triangle's area is `18`. What is the area of the triangle's incircle?

Answer 1

The area of the incircle is `=5.7u^2`

Explanation:

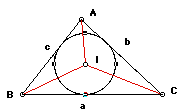
The area of the triangle is `A=18`

The angle `hatA=1/12pi`

The angle `hatB=5/12pi`

The angle `hatC=pi-(1/12pi+5/12pi)=6/12pi=pi/2`

The sine rule is

`a/sinA=b/sinB=c/sinC=k`

So,

`a=ksinA`

`b=ksinB`

`c=ksinC`

Let the height of the triangle be `=h` from the vertex `A` to the opposite side `BC`

The area of the triangle is

`A=1/2a*h`

But,

`h=csinB`

So,

`A=1/2ksinA*csinB=1/2ksinA*ksinC*sinB`

`A=1/2k^2*sinA*sinB*sinC`

`k^2=(2A)/(sinA*sinB*sinC)`

`k=sqrt((2A)/(sinA*sinB*sinC))`

`=sqrt(36/(sin(pi/12)*sin(5/12pi)*sin(1/2pi)))`

`=6/0.5=12`

Therefore,

`a=12sin(1/12pi)=3.11`

`b=12sin(5/12pi)=11.59`

`c=12sin(1/2pi)=12`

The radius of the incircle is `=r`

`1/2*r*(a+b+c)=A`

`r=(2A)/(a+b+c)`

`=36/(26.7)=1.35`

The area of the incircle is

`area=pi*r^2=pi*1.35^2=5.7u^2`