What's the curve parallel to the parabola y=x^2y=x2?
1 Answer
Jun 15, 2017
The parametric equations are
Where k is the distance from
Explanation:
I found a good answer in a forum
I have written the parametric equations into the answer area.
Here is a graph of
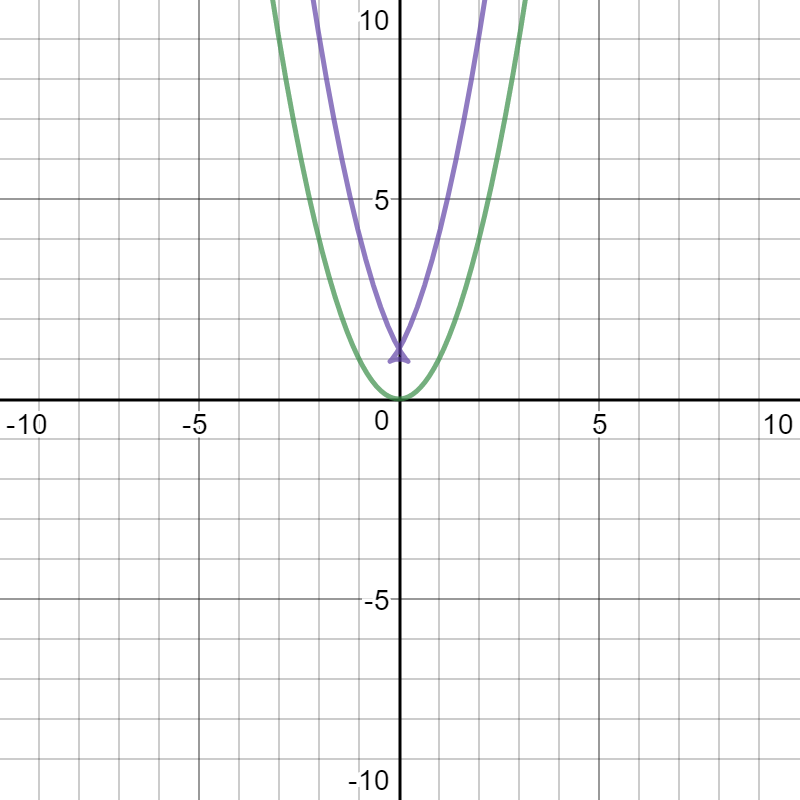 Desmos.com
Desmos.com
Here is a graph of
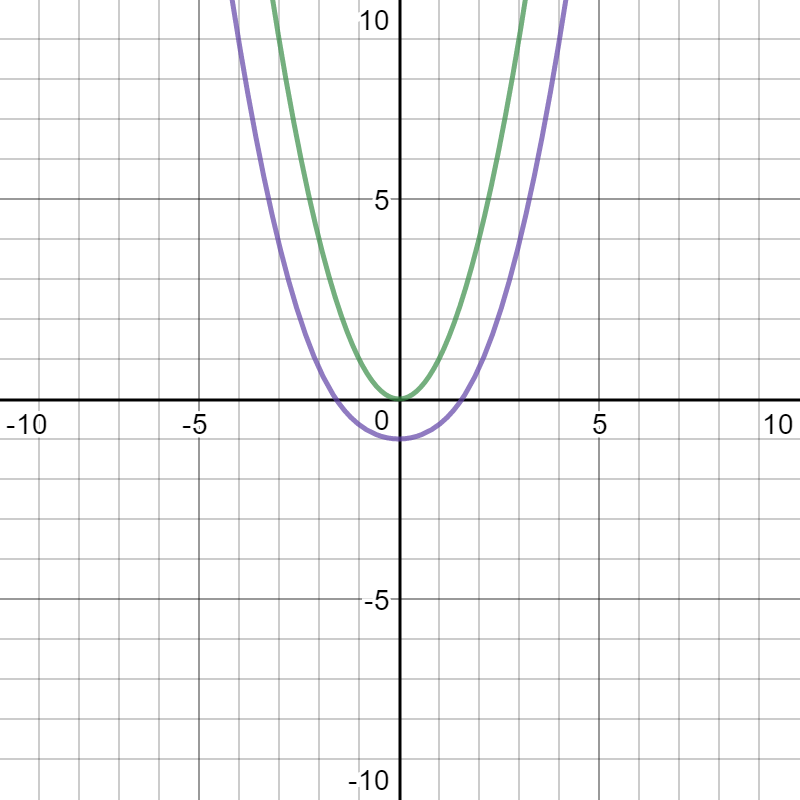 Desmos.com
Desmos.com
