Question #f8d27
2 Answers
Given that the water level varies from 12 inches at low tide to 52 inches at high tide. Low tide occurs at 9:15 a.m. and high tide occurs at 3:30 p.m
So duration of half cycle is
And duration of full cycle is
At low tide height of water level
At high tide height of water level
So equilibrium height of water level
The amplitude or the maximum change from equilibrium level will be
So the cosine function that models the variation in inches above and below the water level as a function of time is given by
The following is the graphical representation of the variation of water level taking
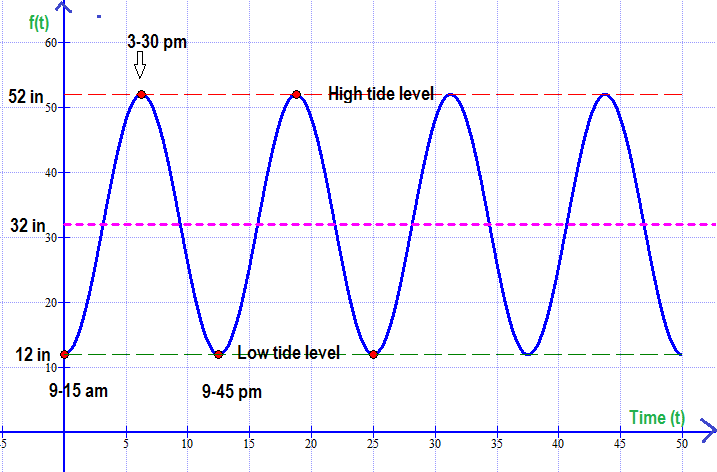
Explanation:
We know that the cosine function has a range of
I'm asuming that in order to have anything below a water level, 12 inches at low tide refers to 12 inches below water level, and similarly 52 inches at high tide refers to above water level.
This means the water varies a total of
If a standard cosine function has a difference of 2, then 32 times that cosine function must have a difference of 64.
Our new cosine function
The next step would be to get the timing right. A standard cosine function varies between its highest and lowest point over a period of
When we look at
So,
Pluging this into our cosine function, we get this:
Let's try it:
So it's not quite there yet, as it starts at its high point, which is not what we want. To counteract this, we need to shift the whole function
The final function will be:
Here's a graph of the function

