Question

Why is the modern-day quantum model of the atom better than John Dalson's model?

Answer 1

First let have a look at John Dalton's model

There is not much hard to understand that it is an atom. John Dalton predicted that all matter is composed of atoms only(even compounds) and atoms are indivisible. And this was not new as the idea of atoms was invented by two Greek philosophers, Democritus and Leucippus in the fifth century BC. The Greek word ατoμoν (atom) means indivisible because they believed that atoms could not be broken into smaller pieces. But now we know that atoms are also composed of electrons, neutrons and protons. Dalton also told that no atom could be changed into another one, created or destroyed.

It is not true that atoms cannot be destroyed. Destroyed in the sense not means that the atom vanishes.
It means that we can break it into neutrons, protons and even electrons by nuclear reactions and other sources of energy like light.And compounds can be changed into other ones to.

Atoms can be created by letting these particles react, like

`"2proton" + "2electron" = H_2`
other sources of energy may be required to start the reaction and this energy is called activation energy

The modern day theory tells that the electrons are situated in orbits around the nucleus which composed of protons and neutrons. It also tells that all orbits are not same and their structure varies from one another.

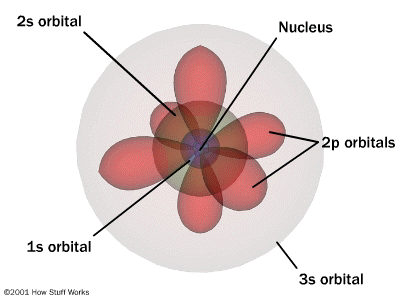
Quantum theory tells us that wave is associated with the properties of the matter.

According to the quantum theory it is impossible to know the exact position and the momentum of an electron in the same time.This is known as Uncertainty principle

`DeltapDeltah ≥ h/(4pi)`

The quantum mechanical model of the atom uses complex shapes of orbitals (sometimes called electron clouds), volumes of space in which there is likely to be an electron. So, this model is based on probability rather than certainty.

Some equations prove this like the

De Brogile equation which tells us that any moving particle has a wavelength

`lamda = h/(mv)`

Four numbers, called quantum numbers, were introduced to describe the characteristics of electrons and their orbitals:

Principal quantum number: n

Angular momentum quantum number: l

Magnetic quantum number: `m_1`

Spin quantum number: `m_s`

Principal quantum number

Principal quantum number n is used to determine the position of the electron shell from the nucleus. The bigger the value of n the electron shell becomes further and more in diameter and more potential energy.It can have positive integer (whole number) values: 1, 2, 3, 4, and so on.

Angular momentum quantum number

The angular momentum quantum number l describes the shape of the orbital, and the shape is limited by the principal quantum number n: The angular momentum quantum number l can have positive integer values from 0 to n–1. For example, if the n value is 3, three values are allowed for l: 0, 1, and 2.

The value of n can be determine from the l.

`l = n-1`

l can be zero or a positive integer less than (n-1)

So there can be multiple values of l

The Electron Spin Quantum Number

Unlike l, n electron spin quantum number `m_s` does not depend on another quantum number. It designates the direction of the electron spin and may have a spin of +1/2, represented by↑, or –1/2, represented by ↓. This means that when `m_s` is positive the electron has an upward spin, which can be referred to as "spin up." When it is negative, the electron has a downward spin, so it is "spin down." The significance of the electron spin quantum number is its determination of an atom's ability to generate a magnetic field or not. (Electron Spin.)

`m_s = +- 1/2`

Magnetic Quantum Number

The magnetic quantum number `m_1` determines the number of orbitals and their orientation within a subshell. Consequently, its value depends on the orbital angular momentum quantum number l . Given a certain l, `m_1` is an interval ranging from -l to +l so it can be zero, a negative integer, or a positive integer.

So if n = 3 what is `m_1`?

If n = 3, l = 0,1,2

For l = 0, `m_1 = 0`

For l = 1, `m_1 = -1, 0, 1`

For l = 2,`m_1 = -2, -1, 0, 1, 2`

Now n can have multiple l but `n_1` cannot have more than 1 sub shell

Because `n -1 = 0`

But other shells ranging from `n_2 to "infinite"`

so subshells are assigned with a certain letter which refer to a particular l value