Question

If an organ pipe is sounded with a tuning fork of frequency 256 Hz, the resonance occured at 35 cm and 105 cm, then the velocity of sound is?

Answer 1

It is an organ pipe with one closed end.

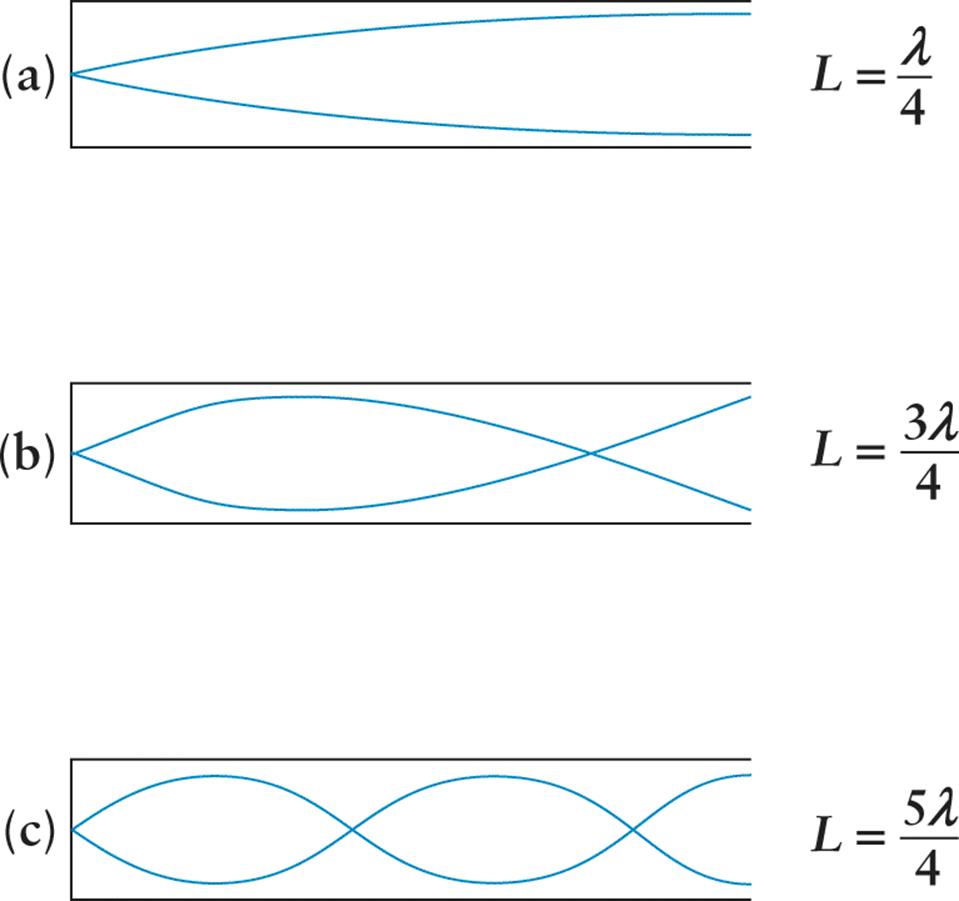
For a close ended organ pipe: The fundamental (first harmonic) needs to have an node at the close end since the air cannot move and an antinode at the open end.

`λ/4 = L_1 + e` …... (1)
where `e` is the end correction.

Another resonance occurs at `L_2=105cm`
For a closed end organ pipe this is the 3rd harmonic resonating as there is no 2nd harmonic for closed ended pipes.

We get

`(3λ)/4 = L_2 + e` …... (2)

Subtracting equations (1) from (2) we get

`λ/2 = (L_2 – L_1)` …... (3)

Using the expression

`v=flambda`
where `v` is velocity of sound, `f` is frequency and `lambda` is the wavelength.

we get

`v = 2f (L_2 - L_1)`

Inserting given values we get

`v=2xx256(105-35)`
`=>v=2xx256(105-35)`
`=>v=35840cms^-1`