Question

Question #b1147

Answer 1

`f in [3.94 xx 10^14` `"s"^-1, 7.89 xx 10^14` `"s"^-1]`

Explanation:

To solve this problem, we can use the equation

`lambdaf = c`

where

• `lambda` (lowercase Greek letter lambda) is the wavelength of the wave, in `"m"`

• `f` if the frequency of the wave, in `"s"^(-1)` (the same as hertz, `"Hz"`

• `c` is the speed of light in vacuum, precisely `299, 792, 458` `"m/s"`

We want to know the range of frequency values where the wavelengths range from `3800` to `7600` `"Å"`. Know that wavelength and frequency are inversely proportional, so the largest wavelength value has the lowest frequency value, and vice versa.

Since the wavelengths must be in meters, we must convert them to meters, knowing that `1` `"m"` `= 10^10` `"Å"`:

`7600cancel("Å")((1color(white)(l)"m")/(10^10cancel("Å"))) = 7.6 xx 10^-7` `"m"`

`3800cancel("Å")((1color(white)(l)"m")/(10^10cancel("Å"))) = 3.8 xx 10^-7` `"m"`

And so the minimum and maximum frequencies are

`f = c/lambda`

`f_"min" = (299792458(cancel("m"))/"s")/(7.6xx10^-7cancel("m")) = color(red)(3.94 xx 10^14` `color(red)("s"^-1`

`f_"max" = (299792458(cancel("m"))/"s")/(3.8xx10^-7cancel("m")) = color(blue)(7.89 xx 10^14` `color(blue)("s"^-1`

The range of frequencies is thus

`f in [color(red)(3.94 xx 10^14` `color(red)("s"^-1), color(blue)(7.89 xx 10^14` `color(blue)("s"^-1)]`

Answer 2

Here's what I got.

Explanation:

As you know, the frequency of a photon and its wavelength have an inverse relationship described by the equation

`color(blue)(ul(color(black)(nu * lamda = c)))`

Here

• `lamda` is the wavelength of the photon
• `nu` is the frequency of the photon
• `c` is the speed of light in a vacuum, usually given as `3 * 10^8"m s"^(-1)`

This implies that the photon with the longest wavelength in the visible part of the EM spectrum will have the lowest frequency and the photon with the shortest wavelength will have the highest frequency.

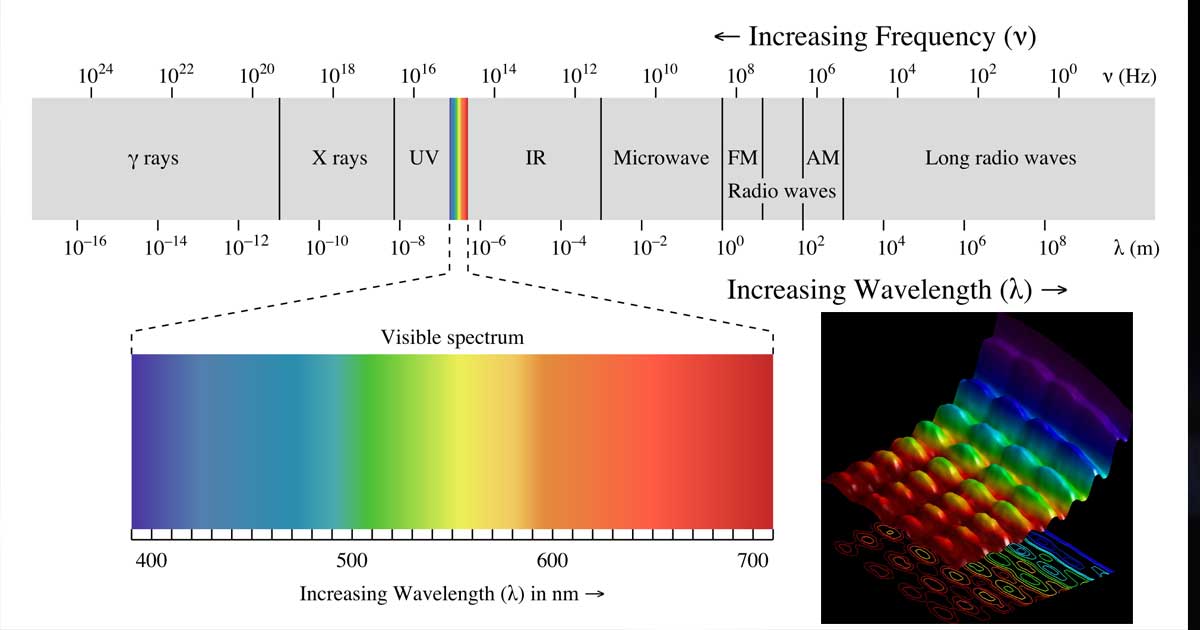
In your case, you will have

`7600 stackrel(@)("A") = "longest wavelength " -> " lowest frequency"`

`3800 stackrel(@)("A") = "shortest wavelength " -> " highest frequency"`

So, start by converting the two wavelengths from angstrom to meters by using the fact that

`1color(white)(.)stackrel(@)("A") = 1 * 10^(-10)` `"m"`

You will end up with

`7600 color(red)(cancel(color(black)(stackrel(@)("A")))) * (1 * 10^(-10)color(white)(.)"m")/(1color(red)(cancel(color(black)(stackrel(@)("A"))))) = 7.6 * 10^(-7)` `"m"`

`3800 color(red)(cancel(color(black)(stackrel(@)("A")))) * (1 * 10^(-10)color(white)(.)"m")/(1color(red)(cancel(color(black)(stackrel(@)("A"))))) = 3.8 * 10^(-7)` `"m"`

Rearrange the equation to solve for `nu`, the frequency of the photon

`lamda * nu = c implies nu = c/(lamda)`

Plug in your values to find

`nu_ 1 = (3 * 10^8 color(red)(cancel(color(black)("m"))) "s"^(-1))/(7.6 * 10^(-7)color(red)(cancel(color(black)("m")))) = 3.9 * 10^14` `"s"^(-1)`

`nu_ 2 = (3 * 10^8 color(red)(cancel(color(black)("m"))) "s"^(-1))/(3.8 * 10^(-7)color(red)(cancel(color(black)("m")))) = 7.9 * 10^14` `"s"^(-1)`

The values are rounded to two sig figs.

Therefore, you can say that the visible portion of the EM spectrum includes electromagnetic radiation that goes from about

`3.9 * 10^(14)color(white)(.)"Hz " -> " corresponds to"color(white)(.)color(red)("RED")`

to about

`7.9 * 10^(14)color(white)(.)"Hz " -> " corresponds to"color(white)(.)color(purple)("VIOLET")`

Notice that the photons with the highest frequency have the shortest wavelength `(color(purple)("VIOLET"))` and the photons with the lowest frequency have the longest wavelength `(color(red)("RED"))`.