Question

`(dy)/(dx) = 3x^2(1+y^2)^(3/2)`?

This is a Calculus 2/3 question that I'm asking for a friend (I'm in Calculus 1).

Answer 1

See below.

Explanation:

To solve the differential equation we can use the property that it is a separable differential equation. So it can be rearranged as

`dy/(1 + y^2)^(3/2) = 3x^2dx`

After integrating both sides we obtain

`y/sqrt(1+y^2)=x^3+C` and finally

`y = pm (x^3+C)/sqrt(1+(x^3+C)^2)`

Answer 2

`y^2 = (x^3+C)^2/(1-(x^3+C)^2)`

Explanation:

We have:

`(dy)/(dx) = 3x^2(1+y^2)^(3/2)`

We can collect term and for a separable differential equation:

`1/(1+y^2)^(3/2) \ (dy)/(dx) = 3x^2`

we can "seperate the variables" to get:

`int \ 1/(sqrt(1+y^2))^3 \ dy = int \ 3x^2 dx`

The RHS is trivially integrable, and the RHS will require a substitution, Let

`y = tan theta => dy/(d theta) = sec^2 theta`

Performing the substitution in the LHS integral, gives:

`int \ 1/(sqrt(1+y^2))^3 \ dy = int 1/(sqrt(1+tan^2theta))^3 \ sec^2theta \ d theta`
`" " = int sec^2 theta/(sqrt(sec^2theta))^3 \ d theta`
`" " = int sec^2 theta/sec^3theta \ d theta`
`" " = int 1/sectheta \ d theta`
`" " = int costheta \ d theta`
`" " = sintheta`
`" " = y/sqrt(1+y^2)`

And so returning to our above equation, and also integrating the RHS, we get:

`y/sqrt(1+y^2) = x^3+C`

We can, in this case, form an explicit solution for `y^2`

`y = (x^3+C)sqrt(1+y^2)`

`:. y^2 = (x^3+C)^2(1+y^2)`
`:. \ \ \ \ = (x^3+C)^2+y^2(x^3+C)^2`

`:. y^2(1-(x^3+C)^2) = (x^3+C)^2`
`:. y^2 = (x^3+C)^2/(1-(x^3+C)^2)`

Answer 3

I got:

`y = tan(arcsin(x^3 + C))`, `" "-1.25992 < x < 0`

For example, `y = tan(arcsin(x^3 + 1))` would be:

---

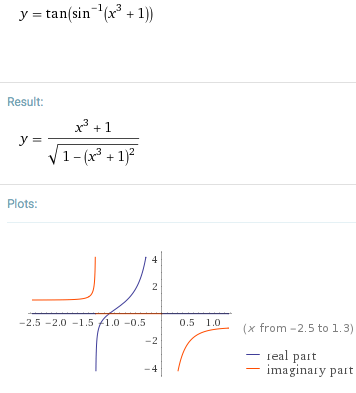
Well, I'm assuming this is supposed to be about differential equations.

The common way to do this is via separation of variables:

`1/(1 + y^2)^(3//2)dy = 3x^2dx`

For this, let `y = tantheta`, so that `dy = sec^2thetad theta`. The left side can then be more easily integrated:

`int (sec^2thetad theta)/((sqrt(1 + tan^2theta))^(3)) = int 3x^2dx`

`=> int cancel((sec^2theta)/(sec^3theta))^(costheta)d theta = int 3x^2dx`

This then gives:

`sintheta = x^3 + C`

Ideally you'd want to get this back into a function `y = f(x)`. One way to do it is to rewrite this as:

`theta = arcsin(x^3 + C)`

Then, since `y = tantheta`, `arctany = theta`, and:

`arctany = arcsin(x^3 + C)`

`=> color(blue)(y = tan(arcsin(x^3 + C)))`

CHECK

Let's see if this even works. If it does, the derivative ought to give the right-hand side. Try taking the derivative with respect to `x`.

`(dy)/(dx) = sec^2(arcsin(x^3 + C)) cdot 1/(sqrt(1 - (x^3 + C)^2)) cdot 3x^2`

To simplify this, `arcsin(x^3 + C)` represents an angle, opposite to leg length `x^3 + C` on a right triangle having a hypotenuse of `1`. From the Pythagorean Theorem:

`(x^3 + C)^2 + b^2 = 1^2`

The missing leg length is `b = sqrt(1 - (x^3 + C)^2)`. This is the adjacent leg, so since

`sec^2(arcsin(x^3 + C)) = 1/(cos^2(arcsin(x^3 + C)))`

`= 1/(cos(arcsin(x^3 + C)))^2`,

we can simplify the derivative to:

`(dy)/(dx) = 1/(1 - (x^3 + C)^2) cdot 1/(sqrt(1 - (x^3 + C)^2)) cdot 3x^2`

`= (3x^2)/(1 - (x^3 + C)^2)^(3//2)`

We further wrote that `sintheta = x^3 + C`, so:

`= (3x^2)/(1 - sin^2theta)^(3//2)`

`= (3x^2)/(cos^2theta)^(3//2)`

`= 3x^2(sec^2theta)^(3//2)`

`= 3x^2(1 + tan^2theta)^(3//2)`

`= 3x^2(1 + y^2)^(3//2)` `color(blue)(sqrt"")`

Yep, our general solution works!