Continuous differentiable?
The figure shows two parts of the graph of a continuous differentiable function #f# on [-10,4].
The derivative #f'# is also continuous.
(a) Explain why #f# must have at least one zero in [-10,4].
(b) Explain why #f'# must also have at least one zero in the interval [-10,4]. What are these zeros called?
(c) Make a possible sketch of the function with one zero of #f'# on the interval [-10,4]
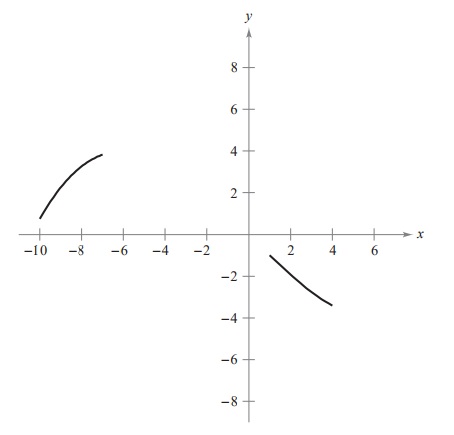
The figure shows two parts of the graph of a continuous differentiable function
The derivative
(a) Explain why
(b) Explain why
(c) Make a possible sketch of the function with one zero of

1 Answer
If you need more details, let me know.
Explanation:
Part a
Part b
From the graph, we can see that the maximum is not at an endpoint, therefore, by Fermat's Theorem, the maximum occurs at a critical number for
We are told that
part c
Connect the endpoints with a smooth curve (no corner points or cusps) that has just one maximum. (One turning point)
Note
Given that the function is differentiable on
Possibly the question=writer intended that we be given:
#f# is continuous on#[-10,4]# and differentiable on#(-10,4)#

