Question

See below (It's about trigonometric functions) Please answer and explain this?

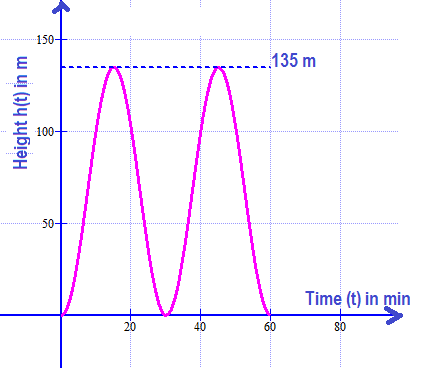
The London Eye has a maximum height of 135 meters, it contains 32 closed cabins, it turns at a constant speed and it takes 30 minutes for one complete tour.

Suppose that the height `h(t)` (in meters) of a cabin of the London Eye as a function of the time `t` (in minutes) can be written as `h(t)=a+bcos⁡(ct)` with `a`, `b` and `c` constants. At time `t=0`the cabin should start at the bottom.

1. Use the data above to find the coefficients `a`, `b` and `c`.
   For `c`, work in radians. Give exact answers.

2. What is the speed of a cabin of the London Eye in meters per second?

For question 1, this is what I have so far :

`h(0)=a+b`
`h(7.5)=a+b*cos(c*7.5)`
`h(15)=a+b*cos(c*15)`

Answer 1

As per problem the movement of the London Eye is periodic one and its height at `t` th instant `h(t)` is given by the following equation

`h(t)=a+bcos(ct)......[1]`, where `h(t)` in meter and t in sec.

Here `c` should be the angular velocity associated with the periodic motion. Again it is also given that time taken by the London Eye to complete one cycle is 3o min. This means time period `T=30min`

Hence `"Angular velocity"=c=omega=(2pi)/T=(2pi)/30=pi/15` rad/min.

So the equation[1] takes the following form

`h(t)=a+bcos((2pi)/30t)......[2]`

Now at `t=0` the London Eye is at the bottom i.e.`h(0)=0`

Applying this condition on [2] we get

`h(0)=a+bcos((2pi)/30xx0)`

`0=a+b=> a+b=0.....[3]`

Since at `t=0` it is at the bottom and it completes the cycle returning at the bottom at `t=30` min,
then we can say that at `t=15` min it will reach at maximum height 135 m i.e. `h(15)=135`m
So we can write

`h(15)=135=a+bcos((2pi)/30xx15)`

`=>a+bcos(pi)=135`

`=>a-b=135.....[4]`

Now adding [3] and [4] we have `2a=135=>a=67.5` m

Subtracting [4] from [3] we get `2b=-135=>b=-67.5`m

So finally the given equation takes the following form

`color(red)(h(t)=67.5-67.5cos((2pi)/30t))`

The variation of height with time can be represented by following graph.