Question

Question #5b2ef

Answer 1

It doesn't. Maybe check the problem to see if it's written differently? Otherwise, this equality is false.

We can solve for `x`, however, and we get that `x = sqrt15/4` for this equation.

Explanation:

Take the inverse cosine of both sides:

`cos(sin^-1(x) - cos^-1(x)) = cos(cos^-1(x/2))`

`cos(sin^-1(x) - cos^-1(x)) = x/2`

Now use the difference rule for cosines:

`cos(a-b) = cos(a)cos(b) + sin(a)sin(b)`

Therefore we can say that:

`cos(sin^-1(x))cos(cos^-1(x)) + sin(sin^-1(x))sin(cos^-1(x)) = x/2`

`cos(sin^-1(x))(x) + (x)sin(cos^-1(x)) = x/2`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
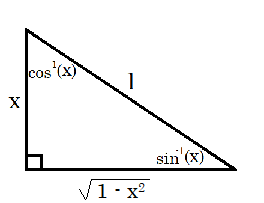
We can write an algebraic expression for `sin(cos^-1(x))` and `cos(sin^-1(x))` using this right triangle:

The sine of the top angle, and the cosine of the bottom angle, are both `sqrt(1-x^2)/1`. Therefore,

`sin(cos^-1(x)) = cos(sin^-1(x)) = sqrt(1-x^2)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

And now we can substitute this into our first equation:

`sqrt(1-x^2)(x) + (x)sqrt(1-x^2) = x/2`

`2xsqrt(1-x^2) = x/2`

Hmm... this isn't starting to look equal. Let's divide both sides by `2x` and see what happens.

`sqrt(1-x^2) = 1/4`

`1-x^2 = 1/16`

`15/16 = x^2`

`+-sqrt15/4 = x`

Well, we've shown that this equation is ONLY true for certain values of `x`, which means that this equality does not always hold true. I would check the problem to see if you might have entered it wrong, or maybe this is a trick proof designed to test your ability to prove something false.

Either way, it's worth noting that the inverse cosine function is only defined for `x=0` to `x=pi`, so the solution `x = -sqrt15/4` isn't valid. Therefore, we have one and only one solution to this inequality:

`x = sqrt15/4`

Final Answer