Question

Optimization Problem?

1. The management of a large store wishes to add a fenced-in rectangular storage
yard of 20,000 square feet, using the building as one of the sides of the yard. Find
the minimum amount of fencing that must be used to enclosed the remaining 3
sides of the yard.

** It is NOT sufficient to find an answer that you think is a max or a min without testing for relative extrema. You MUST test relative extrema at all times by using either the first or second derivative test even if you only have one critical value/point.

Answer 1

Minimum perimeter = `400` feet

Explanation:

Denote the length of the fence by `y` and width by `x`, the area by `A` and the perimeter by `P` as shown:

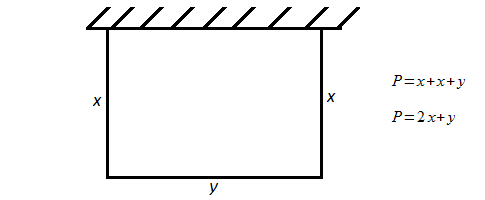
Area is `20,000`, and so:

`xy = 20000`

Perimeter is three sides:

`P = 2x+ y`
`\ \ = 2x+ 20000/x`

We want to minimize `P` wrt `x`. Differentiating wrt `x` we get:

`(dP)/(dx) = 2 - 20000/x^2`

At a minimum or maximum, the derivative will vanish:

`(dP)/(dx) = 0 => 2 - 20000/x^2 = 0`

`:. 10000/x^2 = 1`

`:. x^2 = 10000/x^2`
`:. x^2 = 10000`
`:. \ \ x = 100`

Using `xy=20000` we get:

`100y = 20000 => y = 200`

And:

`P = 2x+y = 200 + 200 = 400`

We need to validate the values `x=100` and `y=200` corresponds to a minimum, by looking at the second derivative:

`(dP)/(dx) = 2 - 20000/x^2`

Differentiating again wrt `x` we get:

`(d^2P)/(dx^2) = 40000/x^3`

And when `x=100 => (d^2P)/(dx^2) > 0` corresponding to a minimum .