A regular hexagon is inscribed in a circle with a radius of 18. Find the area of the shaded region to the nearest TENTH. Note: do NOT round until the end Hello, I need help finding the answer to this question can some one help me?

enter image source here

2 Answers
Fleur
Jul 26, 2017

#176.1# #"units"^2#

Explanation:

#A_"shaded"=A_"circle" - A_"hexagon"#

#A_"circle"=pir^2#
#=pi*18^2#
#=color(blue)(324pi)#

We can split up the hexagon into 6 regular triangles.

#A_"hexagon"= 6 * A_"triangle"#
#=6 * 1/2 b h#

Since the triangles are regular, the base is equal to the radius, #18#. We can represent the height by taking one of the triangles and drawing a line down the middle. The newly formed triangle is a #30°-60°-90°# right triangle.

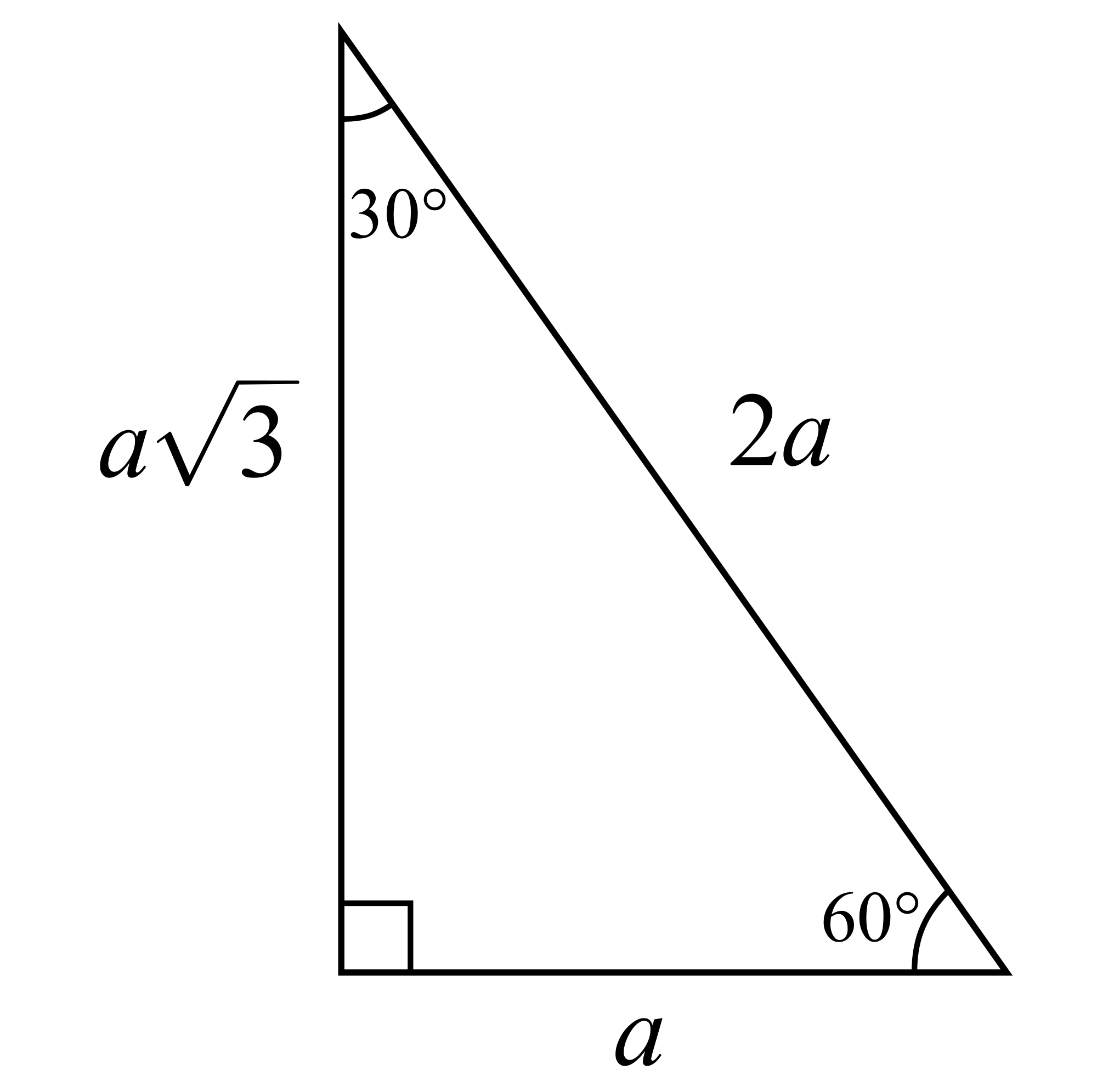
https://commons.wikimedia.org/wiki/Category:30-60-90_triangles

In this case, #a=18/2=9#, so #h = asqrt3 = 9sqrt3#. We can substitute these values into the formula.

#=6*1/2*18*9sqrt3#
#=color(blue)(486sqrt3)#

So, #A_"circle"=324pi# and #A_"hexagon"=486sqrt3#.

#A_"shaded"=A_"circle" - A_"hexagon"#
#=324pi - 486sqrt3#
#=176.1# #"units"^2#

EZ as pi
Jul 26, 2017

#176.1#

Explanation:

The area of the circle can be found using the radius given as #18#.

#A = pi r^2#

#A = pi(18)^2 = 324 pi#

A hexagon can be divided into #6# equilateral triangles with sides of length #18# and angles of #60°#

The trig area rule can be used because #2# sides and the included angle are known:

Area hexagon = #6 xx 1/2 (18)(18)sin60°#

#color(white)(xxxxxxxxx)=cancel6^3 xx 1/cancel2 cancel324^162 xxsqrt3/cancel2#

#color(white)(xxxxxxxxx)=486sqrt3#

Shaded area = area circle - area hexagon

#=324pi -486sqrt3#

#=162(2pi -3sqrt3)#

#=176.0993273" "rarr 176.1#

Related questions
Impact of this question
37914 views around the world
You can reuse this answer
Creative Commons License