Solve for #d#:
First, subtract #color(red)(1/2)# from each side of the equation to isolate the #d# term while keeping the equation balanced:
#d/3 + 1/2 - color(red)(1/2) = 1/(3a) - color(red)(1/2)#
#d/3 + 0 = 1/(3a) - 1/2#
#d/3 = 1/(3a) - 1/2#
Now, multiply each side of the equation by #color(red)(3)# to solve for #d# while keeping the equation balanced:
#color(red)(3) xx d/3 = color(red)(3)(1/(3a) - 1/2)#
#cancel(color(red)(3)) xx d/color(red)(cancel(color(black)(3))) = (color(red)(3) xx 1/(3a)) - (color(red)(3) xx 1/2)#
#d = (cancel(color(red)(3)) xx 1/(color(red)(cancel(color(black)(3)))a)) - 3/2#
#d = 1/a - 3/2#
If necessary, we can subtract the fractions by putting them over common denominators:
#d = (2/2 xx 1/a) - (a/a xx 3/2)#
#d = 2/(2a) - (3a)/(2a)#
#d = (2 - 3a)/(2a)#
Solve for #a#:
First, put the fractions on the left side of the equation over common denominators so they can be added:
#(2/2 xx d/3) + (3/3 xx 1/2) = 1/(3a)#
#(2d)/6 + 3/6 = 1/(3a)#
#(2d + 3)/6 = 1/(3a)#
Next do a cross product or cross multiply the equation:
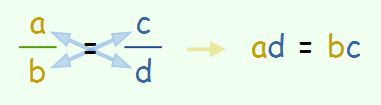
#(3a)(2d + 3) = 6 * 1#
#(3a)(2d + 3) = 6#
Then, divide each side of the equation by #(color(red)(2d + 3))# to isolate the #a# term while keeping the equation balanced:
#((3a)(2d + 3))/(color(red)(2d + 3)) = 6/(color(red)(2d + 3))#
#((3a)color(red)(cancel(color(black)((2d + 3)))))/cancel((color(red)(2d + 3))) = 6/(2d + 3)#
#3a = 6/(2d + 3)#
Now, divide each side of the equation by #color(red)(3)# to solve for #a# while keeping the equation balanced:
#(3a)/color(red)(3) = 6/(color(red)(3)(2d + 3))#
#(color(red)(cancel(color(black)(3)))a)/cancel(color(red)(3)) = 2/(2d + 3)#
#a = 2/(2d + 3)#

