Question

Question #c0aa7

Answer 1

Displacement does have practical uses..

Explanation:

This is my interpretation of your question (let me know if it is incorrect).

Displacement is one of the most basic and fundamental vectors there are, and has both and a magnitude and direction pointing from the initial position to the final position of a particle (regardless of the path taken):

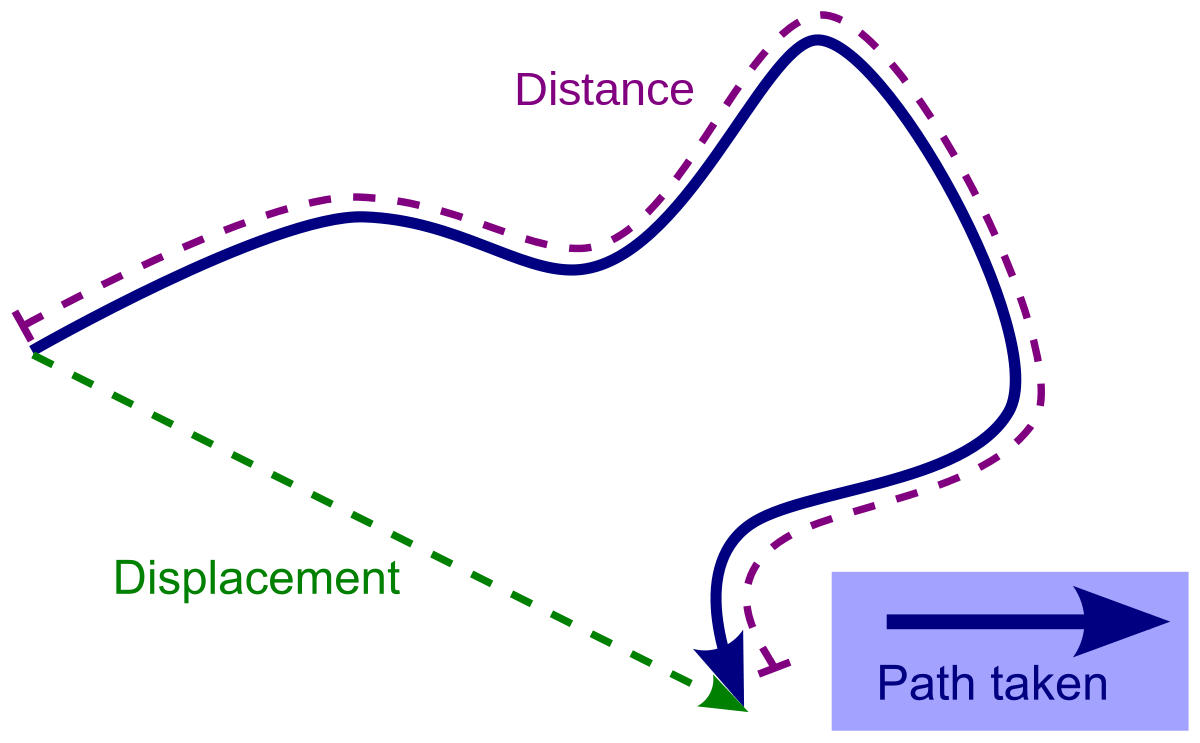
Here, the `sfcolor(blue)("blue"` line represents the `sfcolor(blue)("distance traveled/path taken"` by the particle, and the `sfcolor(green)("green"` line represents the `sfcolor(green)("displacement"` of the particle.

The displacement of a particle is the net change in the position vectors of that particle between two measured points.

`overbrace(Deltavecr)^"displacement" = overbrace(vecr_f)^"final position vector" - overbrace(vecr_i)^"initial position vector"`

Let's look at some practical uses of the displacement vector...

(1) Velocity (average and instantaneous)

• The average velocity of a particle is a vector quantity that describes the rate and direction of change of the position of the particle within a time interval.

The equation is

`overbrace(vecv_"av")^"average velocity" = (overbrace(Deltavecr)^"displacement")/(underbrace(Deltat)_"time interval")`

The following image shows this in component form (you must split into components to perform vector operations):

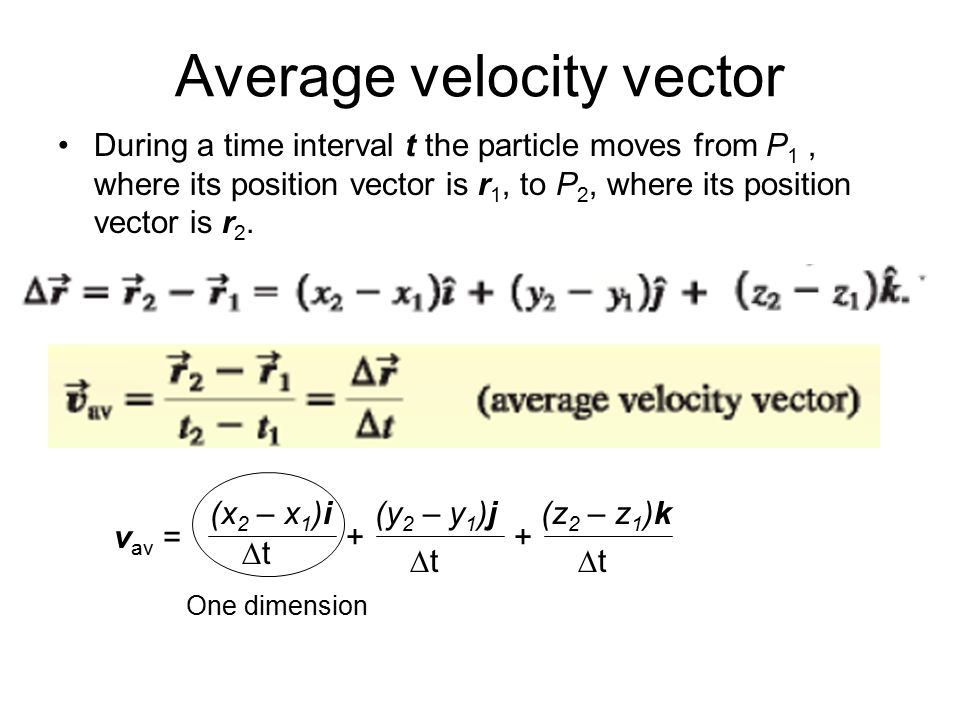
• The instantaneous velocity of a particle describes the instantaneous rate (and direction) of change of position of the particle:

`vecv = (dvecr)/(dt) = lim_(Deltatrarr0) [(Deltavecr)/(Deltat)]`

The below image shows a visual representation of instantaneous velocity:

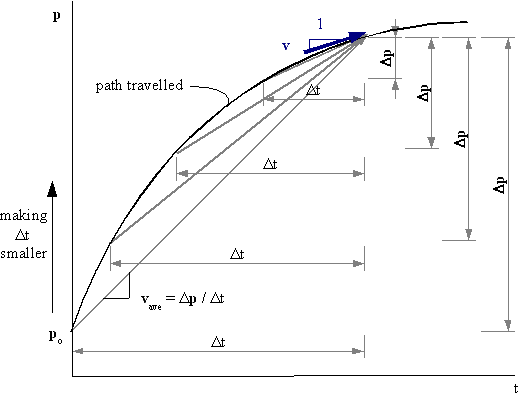
We can see that the instantaneous velocity of a particle at a point is the slope of the tangent line of the position graph at that point.

(2) Work

Work is a scalar quantity that essentially describes the effect of a force acting on a particle as that particle undergoes displacement via that force.

It is a scalar quantity because it is the dot product of the force vector and displacement vector:

`W = vecF · vecs`

(`vecs` is another form of the displacement vector rather than `vecr`)

From the mathematics behind a dot product, if the force acts in a direction perpendicular to its displacement vector, that force does no work on the object.

Furthermore, if a force is applied to an object and the object does not move at all, that force also does no work on the object.

These are just two quite common examples of when displacement is used, and it is certainly fundamental in motion...