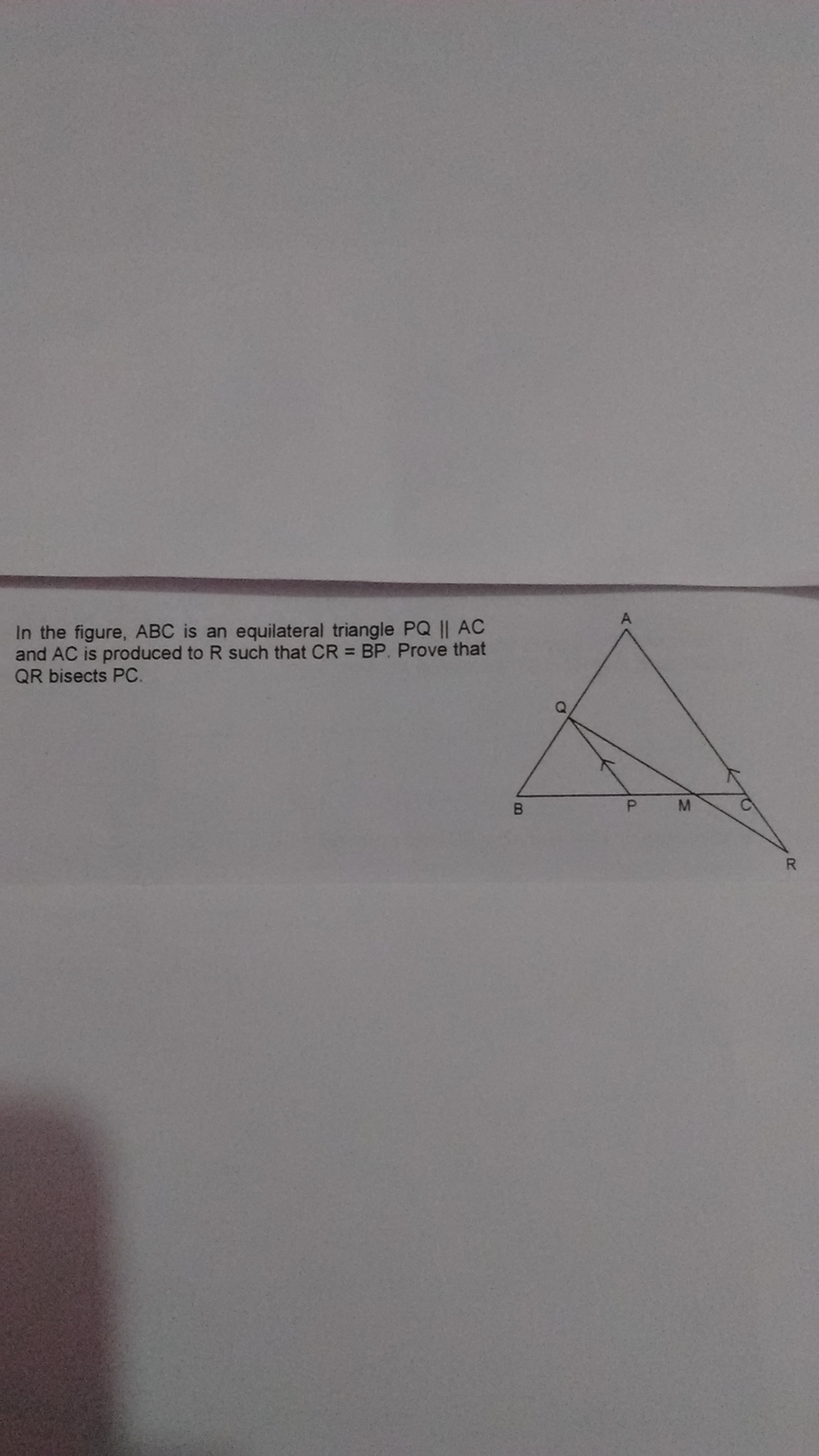
Calling
A=(rho/2,rho sqrt3/2)
B=(0,0)
C=(rho,0)
we have
{(Q = B + lambda_1 (A - B)),(
P = B + lambda_1 (C - B)),(
R = A + (1 + lambda_2) (C - A)),(
s_1 = P + mu_1 (C - P)),(
s_2 = Q + mu_2 (R - Q)):}
Here 0 le lambda_i le 1 and 0 le mu_i le 1
To know if s_1 and s_2 intersect is necessary and sufficient that the equation
s_1 = s_2 or
P + mu_1 (C - P)=Q + mu_2 (R - Q)
have a solution with mu_1^@, mu_2^@ such that
0 le mu_i^@ le 1
but the system
P + mu_1 (C - P)=Q + mu_2 (R - Q)
after the pertinent substitutions reads
(((2 lambda_1-2) rho, (2 - lambda_1 + lambda_2) rho),(0, (lambda_1 +
lambda_2) rho))((mu_1),(mu_2)) = ((lambda_1 rho),(lambda_1 rho))
and solving for mu_1,mu_2 we obtain
(mu_1^@,mu_2^@) = (lambda_1/(lambda_1 + lambda_2), lambda_1/(lambda_1 + lambda_2))
then as can we see
0 le mu_i^@ le 1 and then segments s_1 and s_2 intersect.