Question

Question #5a794

Answer 1

`"initial velocity" = 19.6` `"m/s"`

`"final velocity" = -19.6` `"m/s"`

Explanation:

We're asked to find the initial and final velocities of an object, given that its maximum height is `19.6` `"m"`.

We realize that when a particle is at its maximum height, its instantaneous `y`-velocity `v_y` is zero.

With that being said, we can use the kinematics equation

`ul((v_y)^2 = (v_(0y))^2 + 2a_y(y - y_0)`

where

• `v_y` is the `y`-velocity

• `v_(0y)` is the initial `y`-velocity (what we're trying to find)

• `a_y` is the vertical acceleration, equal to `-g`, or `-9.8` `"m/s"^2`

• `y` is the height (maximum height, in meters)

• `y_0` is the initial height (ground level, `0` `'m"`)

We know:

• `v_y = 0`

• `v_(0y) = ?`

• `a_y = -9.8` `"m/s"^2`

• `y = 19.6` `"m"`

• `y_0 = 0` `"m"`

Plugging in known values:

`(0)^2 = (v_(0y))^2 + 2(-9.8color(white)(l)"m/s"^2)(19.6color(white)(l)"m" - 0color(white)(l)"m")`

`0 = (v_(0y))^2 - 384.16color(white)(l)"m"^2"/s"^2`

`v_(0y) = sqrt(384.16color(white)(l)"m"^2"/s"^2) = color(red)(ulbar(|stackrel(" ")(" "19.6color(white)(l)"m/s"" ")|)`

This is the initial velocity of the ball, so now let's find the final velocity, which we can use the same equation for, only this time `y` and `y_0` are both `0` (when it touches the ground again, its height is `0`):

`(v_y)^2 = (19.6color(white)(l)"m/s"^2) + 2(-9.81color(white)(l)"m/s"^2)(0color(white)(l)"m" - 0color(white)(l)"m")`

Which leaves us with

`(v_y)^2 = (19.6color(white)(l)"m/s")^2`

or

`v_y = sqrt((19.6color(white)(l)"m/s")^2)`

Since the object is on its way down as it touches the ground, we take the negative solution of this:

`v_y = color(blue)(ulbar(|stackrel(" ")(" "-19.6color(white)(l)"m/s"" ")|)`

Any speculations as to why the final and initial velocities have the same magnitude?

Answer 2

Consider the diagram

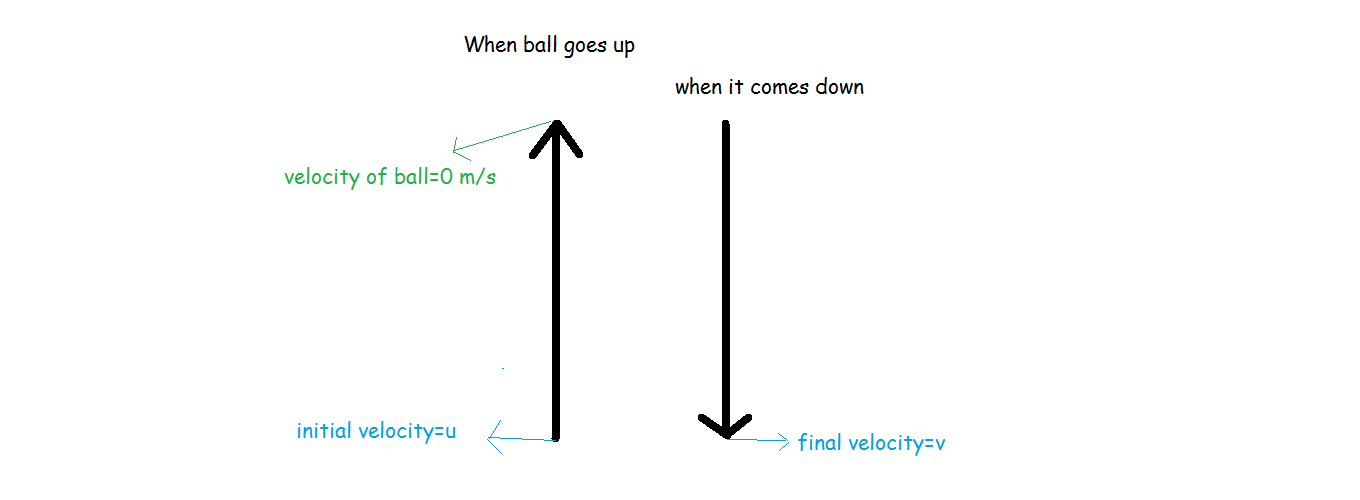
We can solve this question using one of the kinematic equation

`color(brown)(v^2=u^2+2ax`

Where `v` is the final and `u` is the initial velocity.`a` is the acceleration and `x` is the distance travelled

Let's consider the first case

`rArrcolor(orange)(v=0` `("as the ball comes to rest at the maximum height")`

`rArrcolor(orange)(u=?`

`rArrcolor(orange)(a=-9.8 m/s` `("acceleration due to gravity")`

`rArrcolor(orange)(x=19.6m`

Plug all the values in the equation

`rarrv^2=u^2+2ax`

`rarr0^2=u^2+2(-9.8)(19.6)`

`rarr0=u^2+(-384.6)`

`rarr-u^2=-384.6`

`rarru=sqrt(384.6)`

#color (green)(rArr=19.61m/s#

So, the final velocity will be the opposite of the initial velocity `=-19.61m/s`

Hope this helps!