Inverse trig function?
Prove by means of differentiation that if a > 0
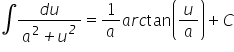
Prove by means of differentiation that if a > 0
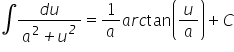
3 Answers
int \ 1/(a^2+u^2) \ du = 1/a arctan(u/a) + C
Explanation:
We want to show:
I = int \ 1/(a^2+u^2) \ du = 1/a arctan(u/a) + C
Method 1 - Differentiation
Let us denote the function by
y =1/a arctan (u/a)
:. ay =arctan (u/a)
:. tan(ay) =u/a
Implicitly differentiating we get:
asec^2(ay)dy/(du) = 1/a
:. sec^2(ay)dy/(du) = 1/a^2
Using the trig Identity
:. (tan^2(ay)+1)dy/(du) = 1/a^2
:. ((u/a)^2+1)dy/(du) = 1/a^2
:. dy/(du) = 1/( a^2 (1+(u/a)^2) )
:. dy/(du) = 1/( a^2 (1+u^2/a^2 )
:. dy/(du) = 1/(a^2+u^2)
Hence we have:
d/du(1/a arctan(u/a) ) = 1/(a^2+u^2)
=> int \ 1/(a^2+u^2) \ du = 1/a arctan(u/a) + C \ \ \ QED
Method 2 - Integration
Although asked to differentiate to form the solution, we can also readily integrate the function:
Let us perform a substitution:
u=a tan theta => (du)/(d theta) = asec^2 theta; \ \ theta = arctan(u/a)
Then provided
I = int \ 1/(a^2+a^2tan^2theta) \ (asec^2 theta) \ d theta
\ \ = 1/a \ int \ (sec^2 theta)/(1+tan^2theta) \ d theta
\ \ = 1/a \ int \ (sec^2 theta)/(sec^2theta) \ d theta
\ \ = 1/a \ int \ d theta
\ \ = 1/a theta + C
And restoring the substitution, we get:
I = 1/a arctan(u/a) + C \ \ \ \ QED
See below.
Explanation:
Now use the chain rule. Note that
= 1/a(1/(1+(u/a)^2) * (1/a))
= 1/(a^2+u^2)
Therefore,
Note
We don't need the restriction
Explanation:
y=1/atan^-1(u/a)+c
rArrdy/(du)=1/axx1/(1+(u/a)^2)xxd/(du)(u/a)
color(white)(rArrdy/du)=1/a^2xx1/(1+(u^2/a^2)
color(white)(rArrdy/du)=1/(a^2+u^2
rArrint(du)/(a^2+u^2)=1/atan^-1(u/a)+ctoa>0


