Question

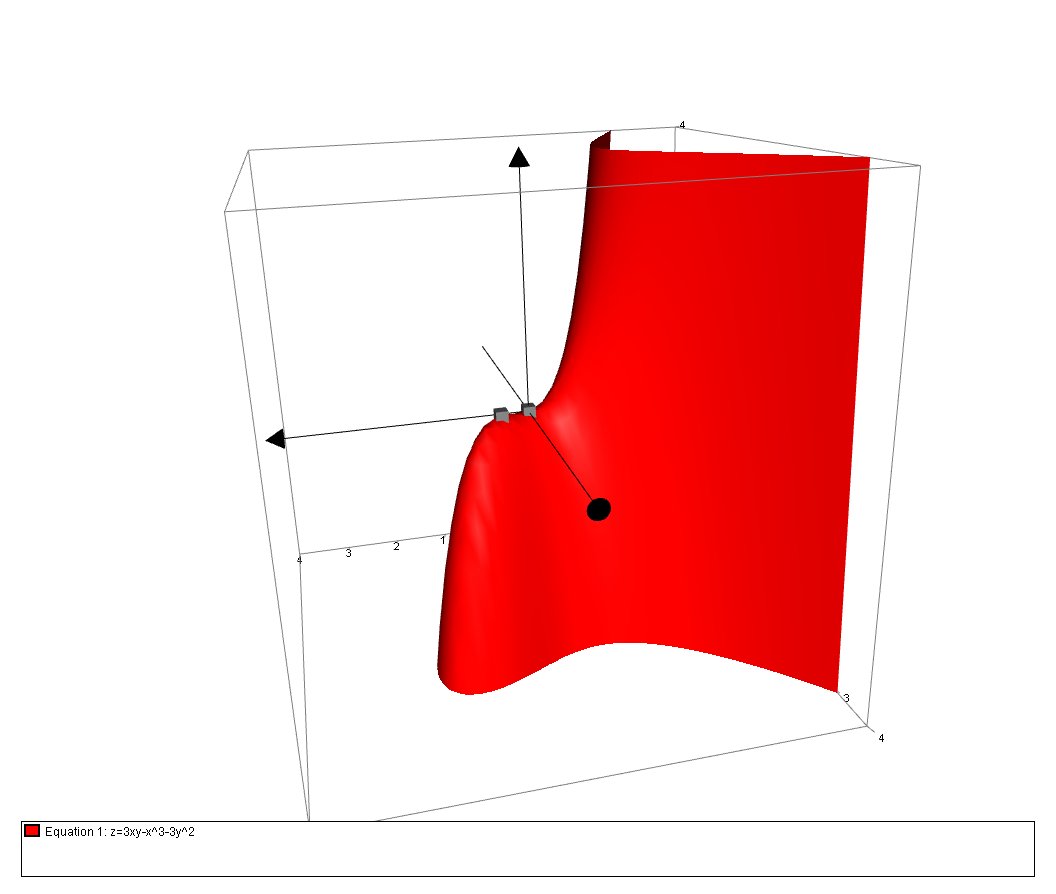
Identify the Critical Points for the function? : `f(x,y) = 3xy-x^3-3y^2`

Answer 1

The saddle point is `(0,0)` and the local maximum is `(1/2,1/4)`

Explanation:

Our function is

`f(x,y)=3xy-x^3-3y^2`

The partial derivatives are

`f_x(x,y)=3y-3x^2`

`f_y(x,y)=3x-6y`

`f_(x x)(x,y)=-6x`

`f_(y y)(x,y)=-6`

`f_(x y)(x,y)=3`

`f_(y x)(x,y)=3`

We look for the critical points

`f_x(x,y)=3y-3x^2=0`, `=>`, `y=x^2`...........`(1)`

`f_y(x,y)=3x-6y=0`, `=>`, `y=x/2`.................`(2)`

We solve for `x` and `y` in equations `(1)` and `(2)`

`x^2=x/2`

`x^2-x/2=0`

`x(x-1/2)=0`

`x=0` and `x=1/2`

Therefore, the critical points are

`(0,0)` and `(1/2,1/4)`

Therefore,

`f_(x x)(0,0)=-6*0=0` and `f_(x x)(1/2,1/4)=-6*1/2=-3`

`f_(y y)(0,0)=-6` and `f_(y y)(1/2,1/4)=-6`

`f_(x y)(0,0)=3` and `f_(x y)(1/2,1/4)=3`

To perform the second derivative test, we calculate the determinant,

`D(0,0) = | (0,3) , (3,-6) |` `= (0) * (-6)-(3) * (3) =-9 <0`, this represents a saddle point

`D(1/2,1/4) = | (-3,3) , (3,-6) |` `= (-3) * (-6)-(3) * (3) =18-9=9>0`, this represents a local maximum as `f_(x x)(1/2,1/4) <0`

Answer 2

`(0,0)`- Saddle Point

`(1/2,1/4)` - Maximum

Explanation:

We have:

`f(x,y) = 3xy-x^3-3y^2`

Step 1 - Find the Partial Derivatives

We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constant. Thus:

The First Derivatives are:

`f_x \ = (partial f) / (partial x) \ \ = 3y -3x^2`
`f_y \ = (partial f) / (partial y) \ \ = 3x-6y`

The Second Derivatives are:

`f_(x x) =(partial^2 f) / (partial x^2) = -6x`
`f_(yy) = (partial^2 f) / (partial y^2) = -6`

The Second Partial Cross-Derivatives are:

`f_(xy) =(partial^2 f) / (partial x partial y) =3`
`f_(yx) = (partial^2 f) / (partial y partial x) =3`

Note that the second partial cross derivatives are identical due to the continuity of `f(x,y)`.

Step 2 - Identify Critical Points

A critical point occurs at a simultaneous solution of

`f_x = f_y = 0 iff (partial f) / (partial x) = (partial f) / (partial y) = 0`

i.e, when:

`3y -3x^2 = 0` ..... [A]
`3x-6y \ \ = 0` ..... [B]

From [A] we have: `y=x^2` so substituting for `y` in [B] we get:

`3x-6x^2 = 0 => 2x^2-x =0`
`:. x(2x-1) = 0`
`:. x=0,1/2`

And the using `y=x^2` we have:

`x=0 \ \ => y = 0`
`x=1/2 => y = 1/4`

So we can conclude that there are two critical points:

`(0,0)`; and `(1/2,1/4)`

Step 3 - Classify the critical points

In order to classify the critical points we perform a test similar to that of one variable calculus using the second partial derivatives and the Hessian Matrix.

`Delta = H f(x,y) = | ( f_(x x) \ \ f_(xy) ) , (f_(yx) \ \ f_(yy)) | = | ((partial^2 f) / (partial x^2),(partial^2 f) / (partial x partial y)), ((partial^2 f) / (partial y partial x), (partial^2 f) / (partial y^2)) | = f_(x x)f_(yy)-(f_(xy))^2`

Then depending upon the value of `Delta`:

`{: (Delta>0, "There is maximum if " f_(x x)<0),(, "and a minimum if " f_(x x)>0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :}`

Using custom excel macros the function values along with the partial derivative values are computed as follows: