Question

What is the length between PO, PQ, OQ have to be when the points form a equilateral triangle?

There are 2 lines on a cartesian axis. One line is defined by `y=2x+1` and point O and Q are an element of it. The other line is described as `y=2x+2` and point P is an element of it. I would appreciate it if you could explain it step by step and in detail.

Answer 1

0.5164

Explanation:

The lines are pictured here. We can visualize the triangle by looking at this graph from another perspective.

Using the properties of equilateral triangles, we can find information about the triangle. Points O and Q are on the lower line and point P is on the upper line. We know that line segments OQ, PQ, and PO are equal in length; we will label this length x. We also know that angles O, P, and Q are 60°, since that is the angle measure of equilateral triangles. We are able to find the value of x through this information.

The length of y is the only length we need to know to solve this triangle. To do this, we need to return to the original graph to find the distance between parallel lines. First, add in a line with a slope of `-1/2`, this is perpendicular to the original lines.

The points of intersection can give the distance between the lines. Let (-0.8,0.4) = a, (-0.4,0.2) = b, and (-0.8,0.2) =c. AC= 0.2 and BC= 0.4 Using the Pythagorean Theorem:
`a^2+b^2=c^2`
`0.2^2+0.4^2=c^2`
`0.2=c^2`
`sqrt0.2=c=y`

The value of x can be found by knowing a 30-60-90 triangle.

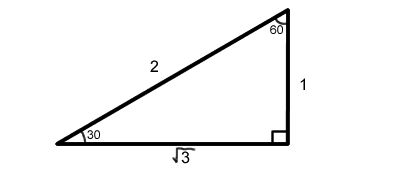
y is proportional to `sqrt3` and x is proportional to 2. We can set up a proportion to find x in terms of y.
`y/sqrt3=x/2`
`x=2y/sqrt3`
Substitute `sqrt0.2` for y and solve:
`x=0.5164`

The length of each side is 0.5164

Answer 2

length`=2/sqrt15` unit

Explanation:

We know that the perpendicular distance `d` between two parallel lines `y=mx+c1, and y=mx+c2` is given by:
`d=|c1-c2|/sqrt(1+m^2)`

Given that the two parallel lines are `y=2x+1, and y=2x+2`, as shown in the figure.
`=> c1=1, c2=2` and slope of the two lines `m=2`
`=> d=PM=|1-2|/sqrt(1+2^2)=1/sqrt5`

Given that `DeltaOPQ` is an equilateral triangle,
`=> OP=PQ=OQ, and angleOPQ=angleOQP=angleQOP=60^@`
`=> POsin60=PM`
`=> PO*sqrt3/2=1/sqrt5`
`=> PO=1/sqrt5*2/sqrt3=2/sqrt15` unit

Hence, length of each side of the equilateral triangle `=2/sqrt15` unit