Question

How do you find the volume bounded by `y=ln(x)` and the lines y=0, x=2 revolved about the y-axis?

Answer 1

For the solution by cylindrical shells, see below.

Explanation:

Here is a picture of the region and a representative slice taken parallel to the axis of rotation.

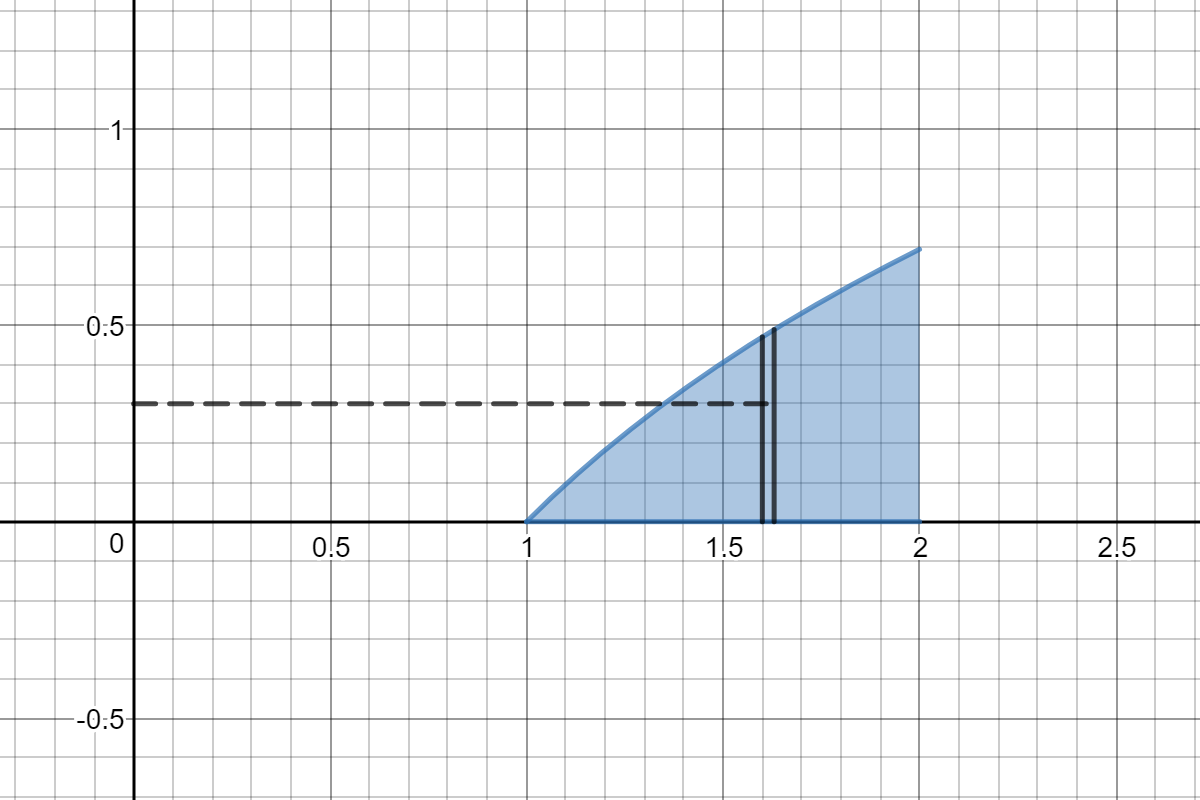
The slice is taken at some value of `x` and has thickness `dx`. So our functions will need to be functions of `x`

Revolving about the `y` axis will result in a cylindrical shell.

The volume of this representative shell is

`2pirh " thickness"`

The radius is shown as a dashed black line in the picture and has length `r = x`

The height of the shell will be the great `y` value minus the lesser `y` value. Since the lesser `y` value is `0`, we have `h = lnx`
As already mentioned, the thickness is `dx`

The representative volume is
`2pixlnxdx`

`x` varies from `1` to `2`, so the solid has volume

`V = int_1^2 2pixlnx dx = 2 pi int_1^2 xlnx dx`

Use integration by parts to get

`= 2pi(2ln2-3/4)`

(Rewrite the answer to taste.)

Answer 2

For the solution by washers see below.

Explanation:

Here is a picture of the region and a representative slice taken perpendicular to the axis of rotation.

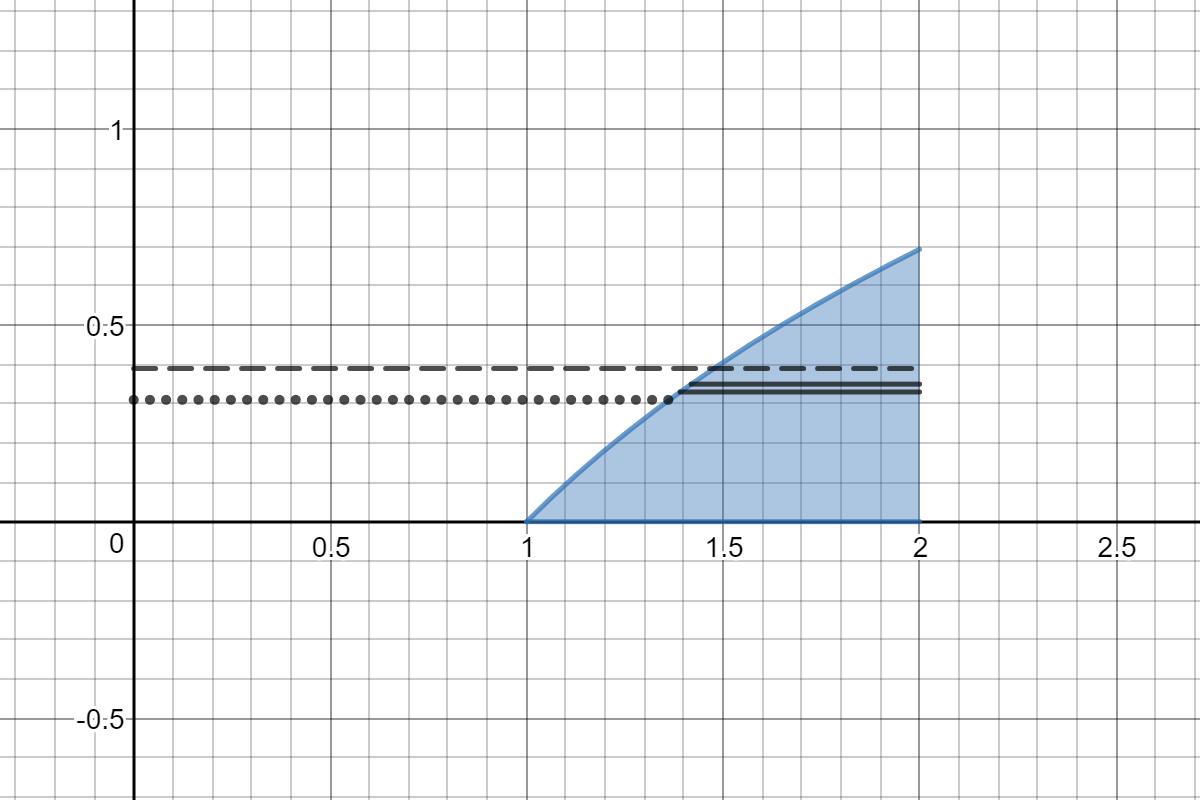
The slice is taken at some value of `y` and has thickness `dy`. So our functions will need to be functions of `y`

The curve `y = lnx` can also be represented by `x = e^y`

Revolving about the `y` axis will result in a washer.

The volume of this representative washer is

`piR^2 *" thickness" - pir^2 " thickness" = pi(R^2-r^2) *" thickness"`

Where `R` is the greater radius -- shown as a dashed line. And `r` is the lesser radius -- shown as a dotted line.

In this case `R = "the "x" value on the right" = 2`
and `R = "the "x" value on the left" = e^y`

The representative volume is
`pi(2^2-(e^y)^2) dy = pi(4-e^(2y))dy`

`x` varies from `1` to `2`,

so `y` varies from `0` to `ln2`

And the volume is

`V = int_0^(ln2) pi(4-e^(2y))dy = piint_0^(ln2) (4-e^(2y))dy`

Use integration to get

`= pi[(4ln2-1/2e^(2ln2))-(-1/2e^0)] = pi(4ln2-3/2)`

(Rewrite the answer to taste.)