The frequency of radiation emitted when electron falls from n=4 to n=1 in a hydrogen atom will be (given ionization energy of H = #2.18 xx 10^(-18) "J/atom"# and #h = 6.626 xx 10^(-34) "J"cdot"s"#)?

1 Answer
Truong-Son N.
Aug 9, 2017

#nu_(4->1) = 3.084 xx 10^(15) "s"^(-1)#

Electronic transitions in the hydrogen atom are given by the Rydberg equation:

#bb(DeltaE = -R_H(1/n_f^2 - 1/n_i^2))#

where:

  • #R_H = 2.18 xx 10^(-18) "J/H atom"# is the Rydberg constant. Yes, it is the ionization energy of hydrogen atom as well!
  • #h = 6.626 xx 10^(-34) "J"cdot"s"# is Planck's constant.
  • #n_k# is the principal quantum number for the #k#th state. Thus, #n_f# indicates the destination energy level, and #n_i# indicates the initial energy level.

So, #n = 4 -> 1# implies #n_f = 1# and #n_i = 4#. This means...

#DeltaE = -2.18 xx 10^(-18) "J/H atom" xx (1/1^2 - 1/4^2)#

which should be negative with respect to the system! (why?)

...and we do indeed get a negative number...

#DeltaE = -2.044 xx 10^(-18) "J/H atom"#

The energy released from the #"H"# atom due to the relaxation process contains photons, which each have energy

#|DeltaE| = E_"photon" = hnu#

where #nu# is the frequency in #"s"^(-1)#.

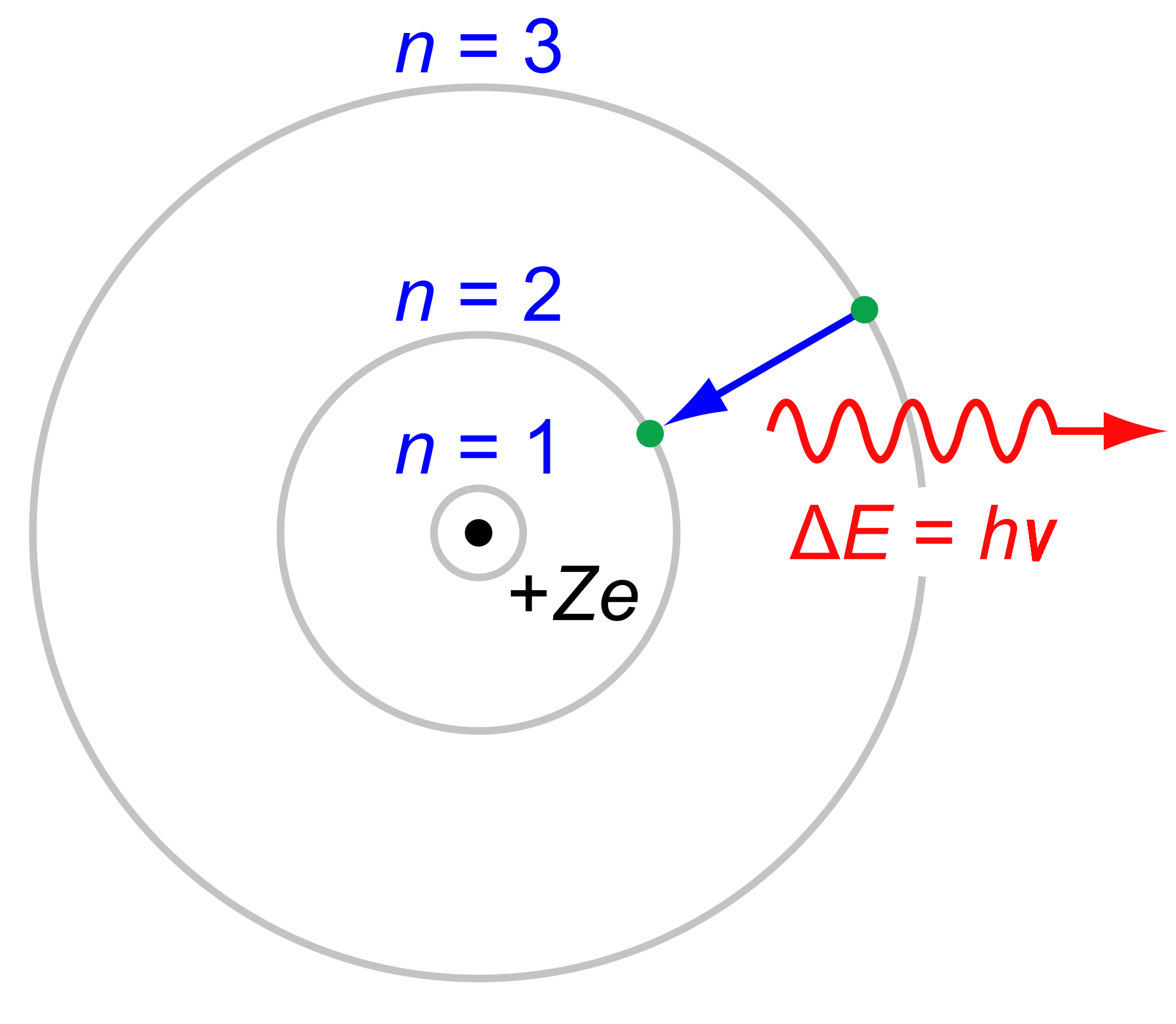
https://upload.wikimedia.org/

Thus, the energy per photon is:

#E_"photon" = +2.044 xx 10^(-18) "J/H atom"#

#= hnu#

and the frequency is therefore:

#color(blue)(nu) = E_"photon"/h = (+2.044 xx 10^(-18) cancel"J"/cancel"H atom" xx cancel"1 H atom"/"photon")/(6.626 xx 10^(-34) cancel"J"cdot"s")#

#= color(blue)ul(3.084 xx 10^(15) "s"^(-1))#

Related questions
See all questions in Calculations with wavelength and frequency
Impact of this question
50529 views around the world
You can reuse this answer
Creative Commons License