Question

What is the equation of the tangent to the curve `x^3 +y^3 +3x-6y=0` at the coordinate `(1,2)`?

Answer 1

Read `"*"` in the question as exponent.

Explanation:

`x^3 +y^3 +3x-6y+9=0`
Gradient is `dy/dx`.
Differentiating the equation with respect to `x`

`3x^2 +3y^2dy/dx +3-6dy/dx=0`
`(3y^2-6)dy/dx =-3x^2-3`
`dy/dx =-(3x^2+3)/(3y^2-6)`
`dy/dx |_("("1,2")")=-(3xx 1^2+3)/(3xx2^2-6)`
`=>=-6/(6)`
`=>=-1`

.-.-.-.-.-.-.-.-
Possible if the equation is

Answer 2

So `(1,2)` does not satisfy the equation as given.

If we modify the equation and use `x^3 +y^3 +3x-6y=0` then So `(1,2)` does satisfy the modified equation then the gradient of the tangent would be `-1`

Explanation:

It has been confirmed in the comments that `(1,2)` is the correct coordinate

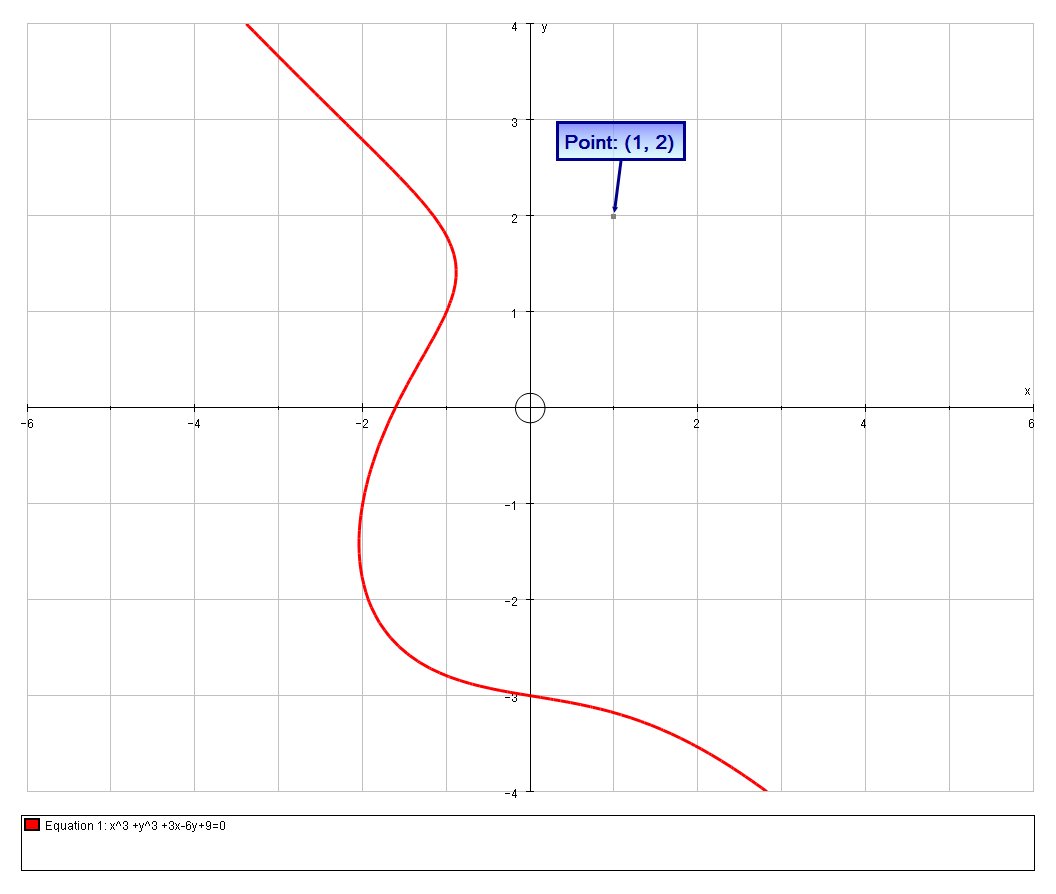
The following will show that in fact it cannot be:

We have:

`x^3 +y^3 +3x-6y+9=0`

With `x=1; y=2` we have:

`LHS = 1+8+3-12+9 = 9 != 0`

So `(1,2)` does not satisfy the equation and therefore does not lie on the curve, hence we cannot find the gradient of the tangent to the curve at that point!

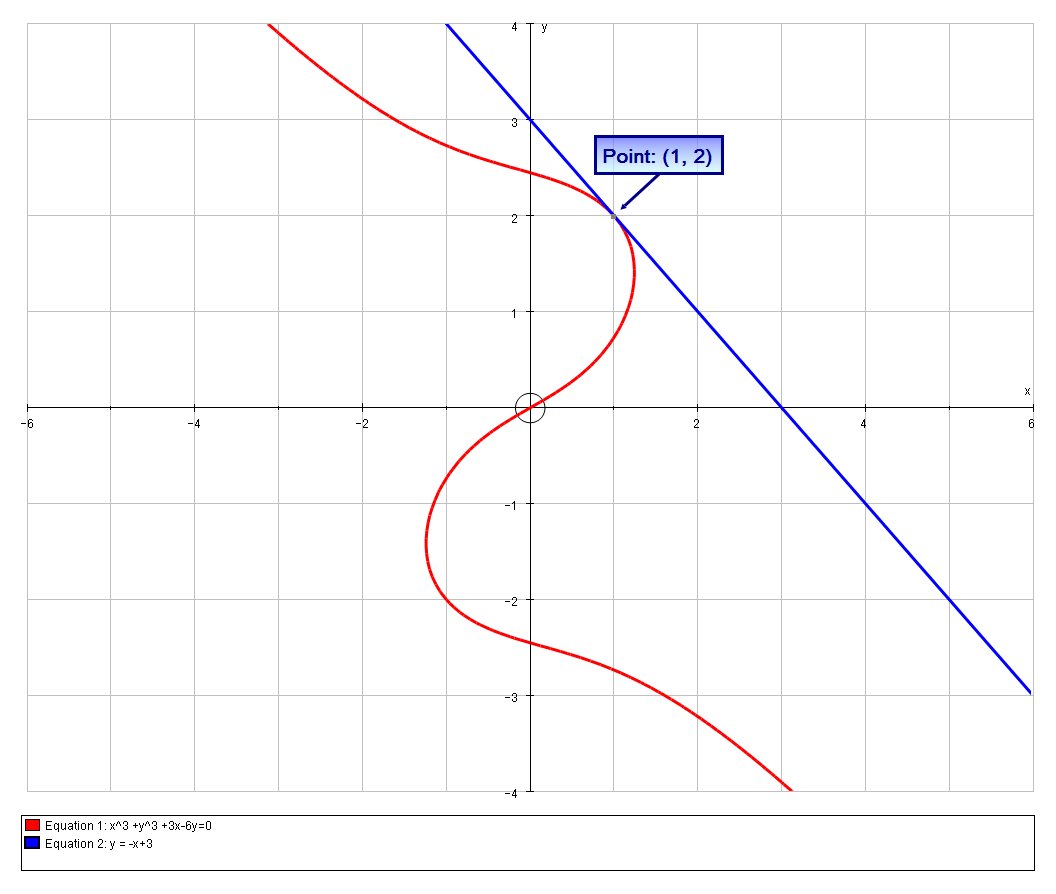
Here is a graph to confirm this visually:

If as Jim H suggests that the correct equation is:

`x^3 +y^3 +3x-6y=0` ..... [A]

Then now with `x=1; y=2` we have:

`LHS = 1+8+3-12 = 0`

So `(1,2)` does satisfy the equation of the modified equation:

Differentiating [A] implicitly we have:

`3x^2 +3y^2dy/dx +3-6dy/dx=0`

We could rearrange this equation and form an explicit expression for `dy/dx`, but this isn't strictly necessary, we just need the value at `(1,2)`
with `x=1; y=2` we have:

`3 +12dy/dx +3-6dy/dx=0`
`:. 6 +6dy/dx=0 => dy/dx = -1`

And this is the gradient of the tangent

We can go on and determine the equation of the tangent

The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is `−1`).

Using the point/slope form `y-y_1=m(x-x_1)`, the tangent equation we seek:

`y - 2 = (-1)(x-1)`
`:. y - 2 = -x+1`
`:. y = -x+3`

The graphs of the equation are: