Question

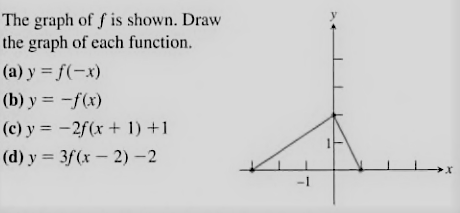
Draw the graph of the functions listed below?

Answer 1

Please see below.

Explanation:

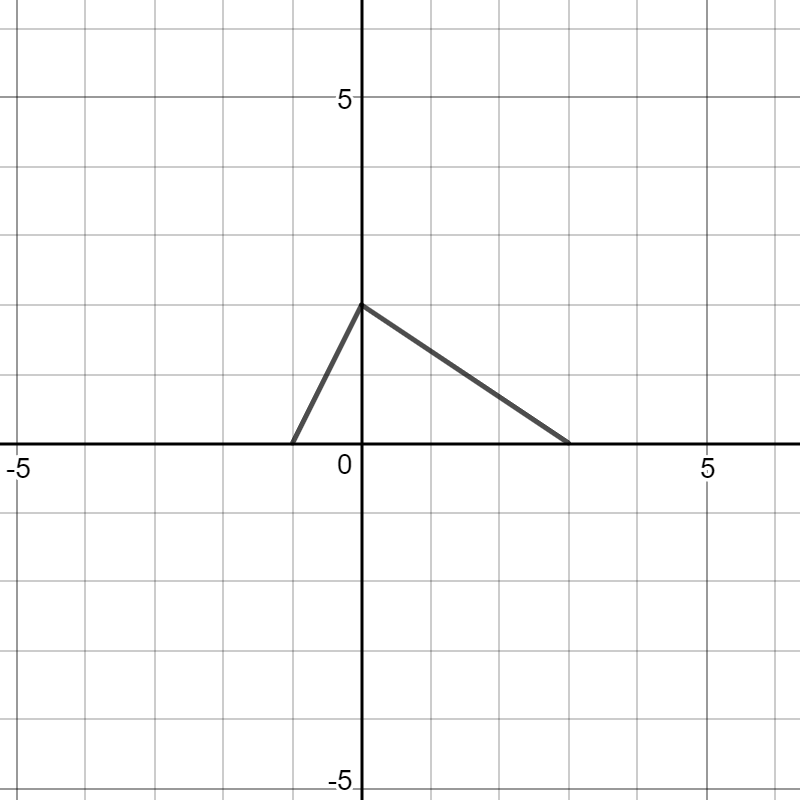
(a) replace `x` by `-x` -- reflect in the `y` axis so

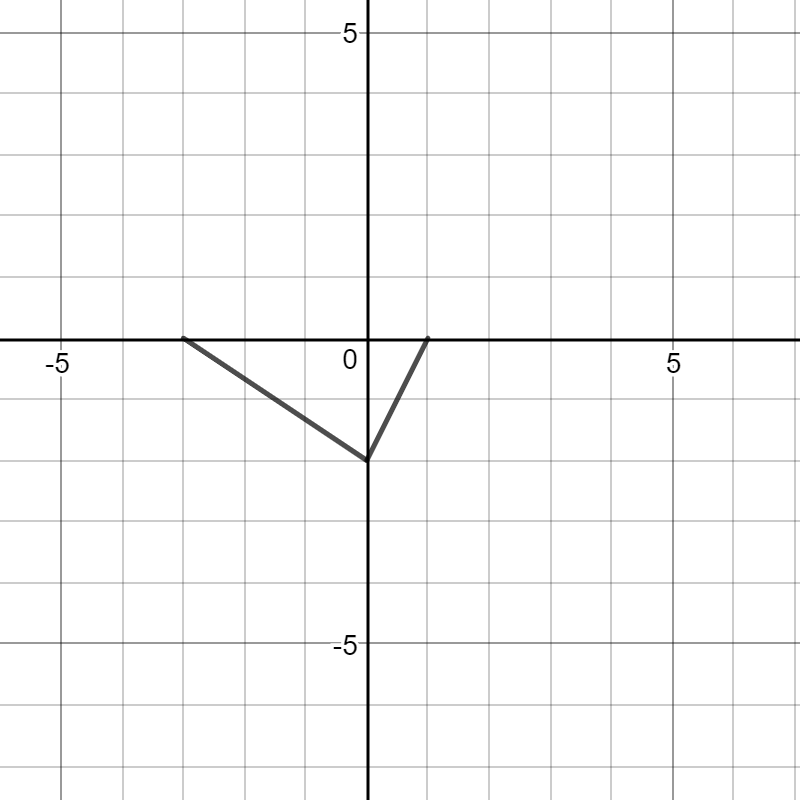
(b) replace `f(x)` by `-f(x)` -- reflect in the `x` axis so

Answer 2

`c` and `d` use the following concepts:

• A negative sign in front of the function means it is flipped vertically, since the function is really `y = f(x)`.
• A constant in front of a function scales it vertically by a factor of that constant.
• If the argument, `x`, in `f(x)`, has `+h`, where `h` is a constant, the function is shifted horizontally by `-h` units. So, the function is shifted in the opposite horizontal direction suggested by the sign of `h`.
• If the function has `k` added to it outside of parentheses, where `k` is a constant, the function is shifted vertically by `k` units.

So, `(c)` is twice as tall, flipped vertically, shifted left by `1`, and up by `1`. In the image below, blue is after scaling the function and then flipping it. Green is after additionally shifting/translating it.

Similarly, `(d)` is three times as tall, and shifted right `2` and down `2`. As before, blue is after just scaling or flipping (in this case, no flipping), and green is after additionally shifting.