#(1+a+b)^2 =3(1+a^2+b^2)# Let's do it???
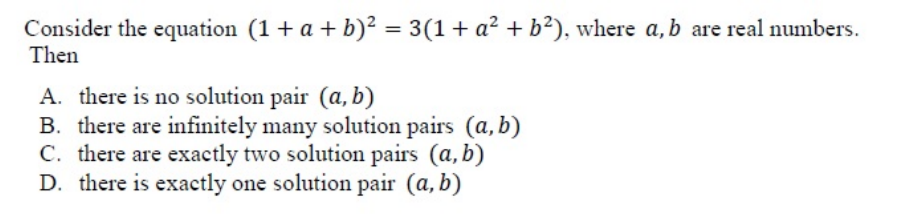
2 Answers
Explanation:
Solving the traditional way
Now solving for
now substituting and solving for
Another way to do the same
but
and concluding
D. There is exactly one solution pair
Explanation:
Given:
#(1+a+b)^2 = 3(1+a^2+b^2)#
Note that we can make this into a nice symmetric homogeneous problem by generalising to:
#(a+b+c)^2 = 3(a^2+b^2+c^2)#
then set
Expanding both sides of this generalised problem, we have:
#a^2+b^2+c^2+2ab+2bc+2ca = 3a^2+3b^2+3c^2#
Subtracting the left hand side from both sides, we get:
#0 = 2a^2+2b^2+2c^2-2ab-2bc-2ca#
#color(white)(0) = a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2#
#color(white)(0) = (a-b)^2+(b-c)^2+(c-a)^2#
For real values of
#a = b = c#
Then putting


