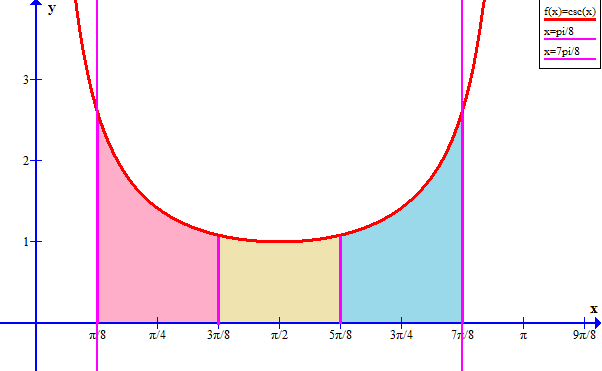
How do you use the Trapezoidal rule and three subintervals to give an estimate for the area between y=cscxy=cscx and the x-axis from x= pi/8x=π8 to x = 7pi/8x=7π8?
2 Answers
Approximately
Explanation:
Dividing the given interval
into 3 equal width intervals (each with a width of
[from this point on, extensive use of spreadsheet/calculator is recommended]
Evaluating
The area of each interval trapezoid is calculated as
Similarly we can calculate
and the Sum of these Areas gives an approximation of the integral value:
int_(pi/8)^((7pi)/8) \ cscx \ dx ~~ 3.7526 \ \ (4dp)
Explanation:
We have:
y = cscx
We want to estimate
Deltax = ((7pi)/8-pi/8)/3 = pi/4
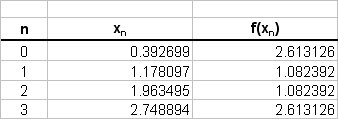
The values of the function, working to 6dp, are tabulated using Excel as follows;
Trapezium Rule
A = int_(pi/8)^((7pi)/8) \ cscx \ dx
\ \ \ ~~ 0.785398/2 * { 2.613126 + 2.613126 + 2*(1.082392 + 1.082392) }
\ \ \ = 0.392699 * { 5.226252 + 2*(2.164784) }
\ \ \ = 0.392699 * { 5.226252 + 4.329569 }
\ \ \ = 0.392699 * 9.555821
\ \ \ = 3.752562
Actual Value
For comparison of accuracy:
A= int_(pi/8)^((7pi)/8) \ cscx \ dx
\ \ \ = [ color(white)(""/"") -log(abs(csc(x)+cot(x))) \ ]_(pi/8)^((7pi)/8
\ \ \ = 3.229781832346191