Two charges of # -6 C # and # -3 C# are positioned on a line at points # -5 # and # 8 #, respectively. What is the net force on a charge of # 4 C# at # 2 #?
1 Answer
The net force is
Explanation:
The force between two charges is given by Coulomb's law:
#|vecF|=k(|q_1||q_2|)/r^2# where
#q_1# and#q_2# are the magnitudes of the charges,#r# is the distance between them, and#k# is a constant equal to#8.99xx10^9" Nm"^2//"C"^2# , sometimes referred to as Coulomb's constant.
- Since unspecified, I'll assume radii values to be in meters so that the units work out.
Here is a diagram of the situation:
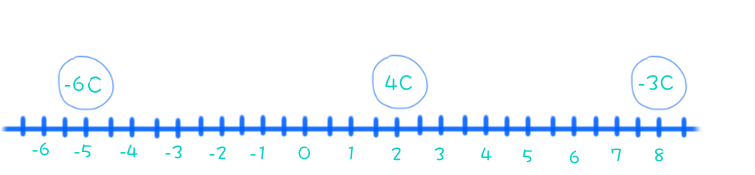
To find the net force on the
We have the following information:
#|->Q_1=-6"C at " -5# #|->Q_2=4"C at " 2# #|->Q_3=-3"C at " 8# #|->k=8.99xx10^9" Nm"^2//"C"^2#
#color(blue)(vecF_("net on 3")=sumvecF=vecF_(1 on 2)+vecF_(3 on 2))#
Recall that like charges repel, while opposite charges attract. Each of the charges acting on
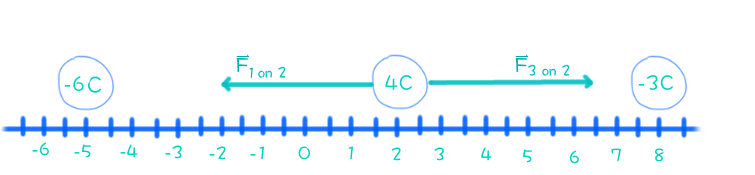
where
#vecF_(1" on " 2)# is the force of#Q_1# on#Q_2# and#vecF_(3" on " 2)# is the force of#Q_3# on#Q_2#
So, we can calculate
#abs(vecF_(1" on " 2))=k*(|q_1||q_2|)/(r_(12)^2)#
#=(8.99xx10^9" Nm"^2//"C"^2)*(6C*4C)/(7"m")^2#
#color(blue)(=4.40xx10^(9)" N")#
#abs(vecF_(3" on " 2))=k*(|q_3||q_2|)/(r_(32)^2)#
#=(8.99xx10^9" Nm"^2//"C"^2)*(3C*4C)/(6)^2#
#color(blue)(=3.00xx10^9" N")#
Therefore, we have:
#color(blue)(vecF_(n e t)=-1.40xx10^9" N")#
That is,
Here is what the forces exerted on charges by other charges of the same or different sign look like:


