Question

An object with a mass of `5 kg` is on a plane with an incline of `pi/8`. If the object is being pushed up the plane with `4 N` of force, what is the net force on the object?

Answer 1

`F_"net"~~15" N"` directed down the plane.

Explanation:

We are given the following information:

• `|->m=5"kg"`
• `|->theta=pi/8`
• `|->F_p=4"N"`

A diagram of the situation:

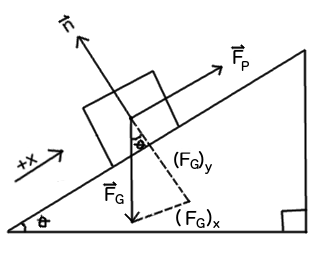
Where `vecn` is the normal force, `vecF_G` is the force of gravity, decomposed into its parallel and perpendicular components, and `vecF_p` is the pushing force.

Note: I will assume a "frictionless" incline based on the information provided.

Let's define up the incline as positive.

We can calculate the net force on the object by summing the parallel (x, horizontal) and perpendicular (y, vertical) components of our forces. We have:

`F_(x" net")=sumF_x=F_p-(F_G)_x=ma_x`

`F_(y" net")=sumF_y=n-(F_G)_y=ma_y`

We can assume dynamic equilibrium vertically, where `a_y=0`. Therefore we have:

`color(darkblue)(F_(x" net")=F_p-(F_G)_x)`

`color(darkblue)(F_(y" net")=0`

Since we're given `F_p`, we need to find the parallel component of `F_G`. This can be accomplished using basic trigonometry. As seen in the above diagram, the angle between the force of gravity and the vertical is equal to the angle of incline.

`sin(theta)="opposite"/"hypotenuse"`

`=>sin(theta)=(F_G)_x/F_G`

`=>(F_G)_x=F_Gsin(theta)`

Because `F_G=mg`:

`=>color(darkblue)((F_G)_x=mgsin(theta))`

Which gives us:

`color(darkblue)(F_(x" net")=F_p-mgsin(theta))`

`color(darkblue)(F_(y" net")=0`

We can now calculate the parallel and perpendicular components of the net force.

`F_(x" net")=F_p-mgsin(theta)`

`=4"N"-(5"kg")(9.81"m"//"s"^2)sin(pi/8)`

`=-14.77"N"`

`~~-15"N"`

• Note that the negative sign indicates direction. We defined up the ramp as positive, so a negative parallel component of the net force tells us that the net force horizontally is down the ramp. In other words, the magnitude of the force of gravity is greater than that of the pushing force.