Question

Find integration of tan^3 3x sec^4 3x dx?

Answer 1

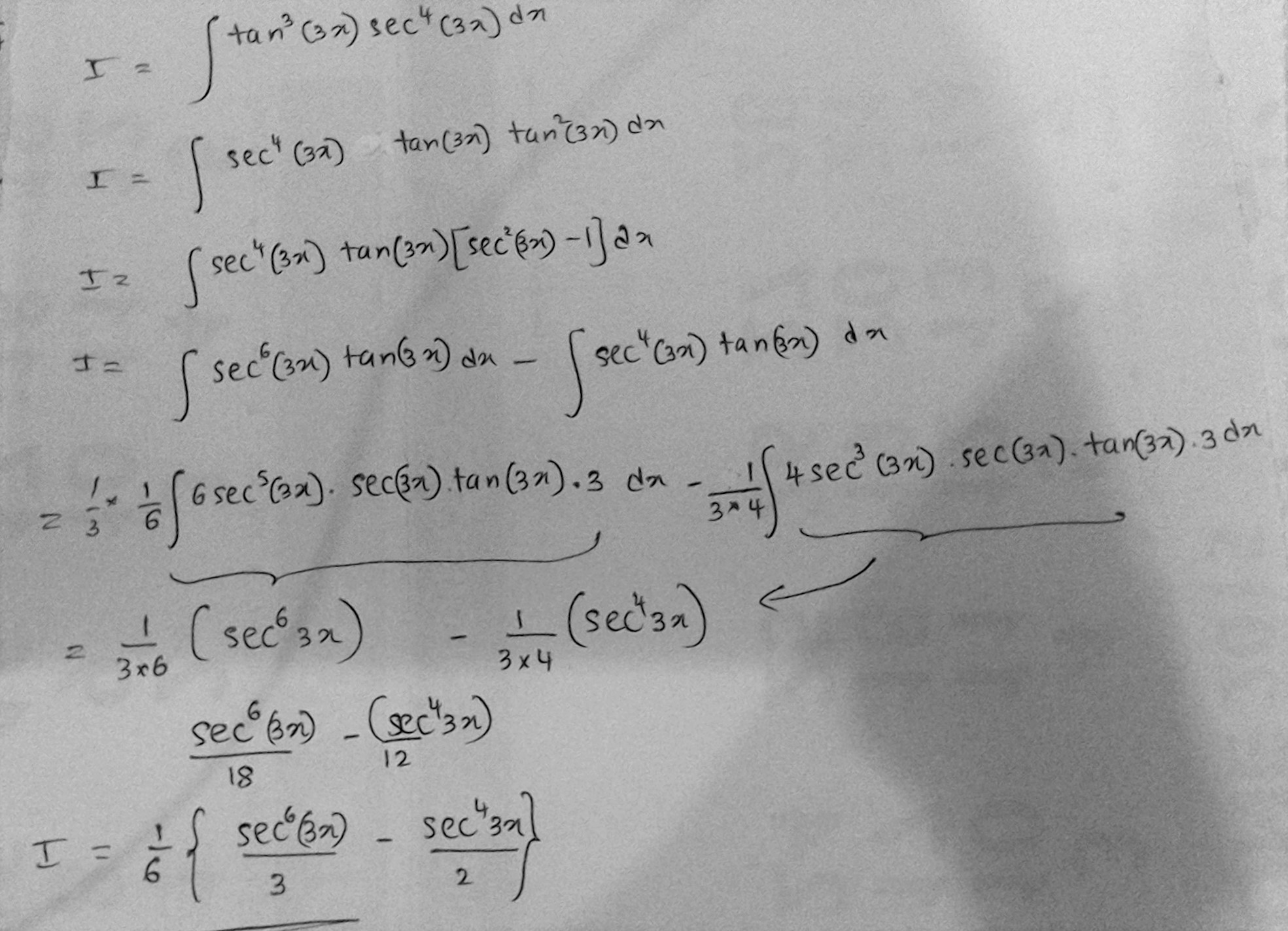
Explanation:

using some trignometric formulae

Answer 2

`int tan^3 3x sec^4 3x dx` can also be written as `(tan^6 3x)/18 + (tan^4 3x)/12 +C`

Explanation:

Another answer sows how to get

`int tan^3 3x sec^4 3x dx = (sec^6 3x)/18 + (sec^4 3x)/12 +C` .

We can use `d/dx(tanx) = sec^2 x` to reason:

`int tan^3 3x sec^4 3x dx = int tan^3 3x (sec^2 3x) sec^2 3x dx`

`= int tan^3 3x (tan^2 3x + 1) sec^2 3x dx`

`= int (tan^5 3x + tan^3 3x) sec^2 3x dx`

`= int (tan^5 3x) sec^2 3x dx + int (tan^3 3x) sec^2 3x dx`

`= 1/3 (tan^6 3x)/6 + 1/3 (tan^4 3x)/4 +C`

`= (tan^6 3x)/18 + (tan^4 3x)/12 +C`