Question

Question #e4fb1

Answer 1

It is at `(2, 4/3)` , where the second derivative of the curve, `(d^2y)/dx^2=x-2` is equivalent to 0, i.e. x=2

Explanation:

Inflection points occur on a function when the curve of the function changes from convex to concave or vice versa, or in other words to direction of curvature changes

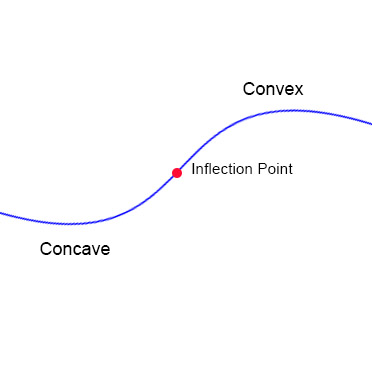
Mathematically, this means that the inflection point is where the second derivative of the curve is 0 , as second derivative represents the rate of change of the derivative, or the slope of the curve at a point. To obtain the second derivative of a function, differentiate the derivative of the function.

In the figure above, in the concave region, the slope gets steeper and steeper, thus the slope increases, and the second derivative, or the rate of change of the slope, is positive. In the convex region, however, the 'steepness' or slope of the curve decreases, thus second derivative is negative. Thus, when the curve changes from concave to convex, the second derivative changes from positive to negative , so at the exact point where the direction of curvature changes, the inflection point, the second derivative is 0