Question

Question #af298

Answer 1

Function f(x) takes the input value of x, multiplies it by `-6`, and then adds 2.

The inverse function reverses this. Take the input value, subtract 2 from it, then divide by -6

Or, `f^-1 (x)= (x-2)/-6`.

You should always verify with some example input values.

Say, x = 2: `f(2) = (-6* 2) + 2 = -10`

`f^-1(-10) = (-10 -2)/-6 = (-12)/-6 = 2`

So, you get back the original input value you put in for f(x).

Try it with some additional values to be sure.

`f(3) = -16`, and `f^-1(-16) = (-18)/-6 = 3`, etc.

Try with some negative values:

`f(-3) = 20`, and `f^-1(20) = -3`, and so on.

Answer 2

`f^-1(x) = -1/6 x + 1/3`.

Explanation:

To find the inverse of `f(x) = -6x +2`, switch the variables `x` and `y` and then solve for `y`.

`y = -6x+2`

`x = -6y + 2` `->` switch the variables

`x - 2 = -6y`

`y = -(x-2)/6`

`y = - 1/6 x + 2/6`

`y = - 1/6 x + 1/3`

So, `f^-1(x) = -1/6 x + 1/3`.

We can verify this by graphing the function and its inverse; `f^-1(x)` should be a reflection of `f(x)` over the line `y=x`.

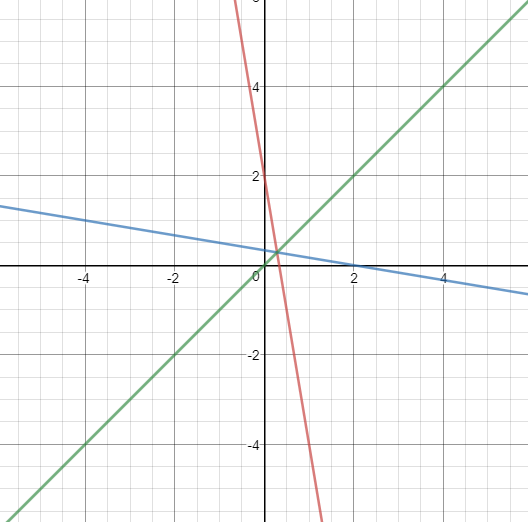
It's clear to see that `f(x)` (red) and `f^-1(x)` (blue) are reflections of one another over `y=x` (green).