A circle has a center at #(1, -2)# and radius of #4#. Does the point #(3.4, 1.2)# lie on the circle?

2 Answers
Fleur
Sep 1, 2017

Yes.

Explanation:

First, find the equation of the circle. The general equation of a circle is #(x-h)^2 + (y-k)^2 = r^2#, where #(h,k)# is the center and #r# is the radius.

Substituting #(1, -2)# for #(h,k)# and #4# for #r#, we get

#(x-h)^2 + (y-k)^2 = r^2#

#(x-color(blue)1)^2 + (y - color(blue)((-2)))^2 = color(blue)4^2#

#(x-1)^2 + (y+2)^2 = 16#

If the point #(3.4, 1.2)# lies on the circle, substituting the point into the equation will still make it valid.

#(x-1)^2 + (y+2)^2 = 16#

#(color(red)3.4 - 1)^2 + (color(red)1.2 + 2)^2 = 16#

#2.4^2 + 3.2^2 = 16#

#5.76 + 10.24 = 16#

#16 = 16#

Thus, #(3.4, 1.2)# does lie on the circle.

Graphing the circle also allows us to verify whether the point lies on it.

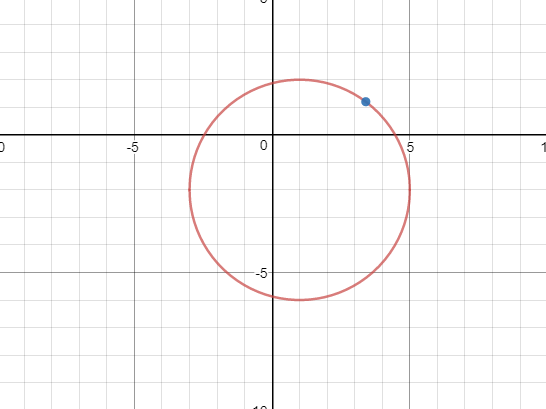
desmos.com

Ratnaker Mehta
Sep 1, 2017

Yes.

Explanation:

Let #C=C(1,-2)# be the Centre, and #r=4# the Radius of the

Circle.

Calling the point #(3.4,1.2)=P,# we find the Distance,

#CP=sqrt{(3.4-1)^2+(1.2-(-2))^2,#

#=sqrt(2.4^2+3.2^2),#

# rArr CP=4=r.#

Hence, the pt. #(3.4,1.2)# is on the Circle.

Related questions
Impact of this question
10532 views around the world
You can reuse this answer
Creative Commons License