Can someone help me out please? Thanks! Please explain 'cause I have more that I want to do on my own :)
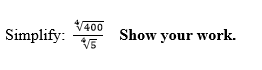
3 Answers
Explanation:
I can't really see the text so I just assumed it was
The first thing I will do is to cancel the
Let's focus on the top part which is
So the numerator would be
Assumption: the question reads as
Explanation:
Look for values raised to the power of 4
 Tony B
Tony B
This gives:
Explanation:
(root(4)(400))/(root(4)(5))=root(4)(400/5)=root(4)(80)
root(4)(80)=root(4)(16xx5)
color(white)(xxx)=root(4)(16)xxroot(4)(5)
color(white)(xxx)=2root(4)(5)


