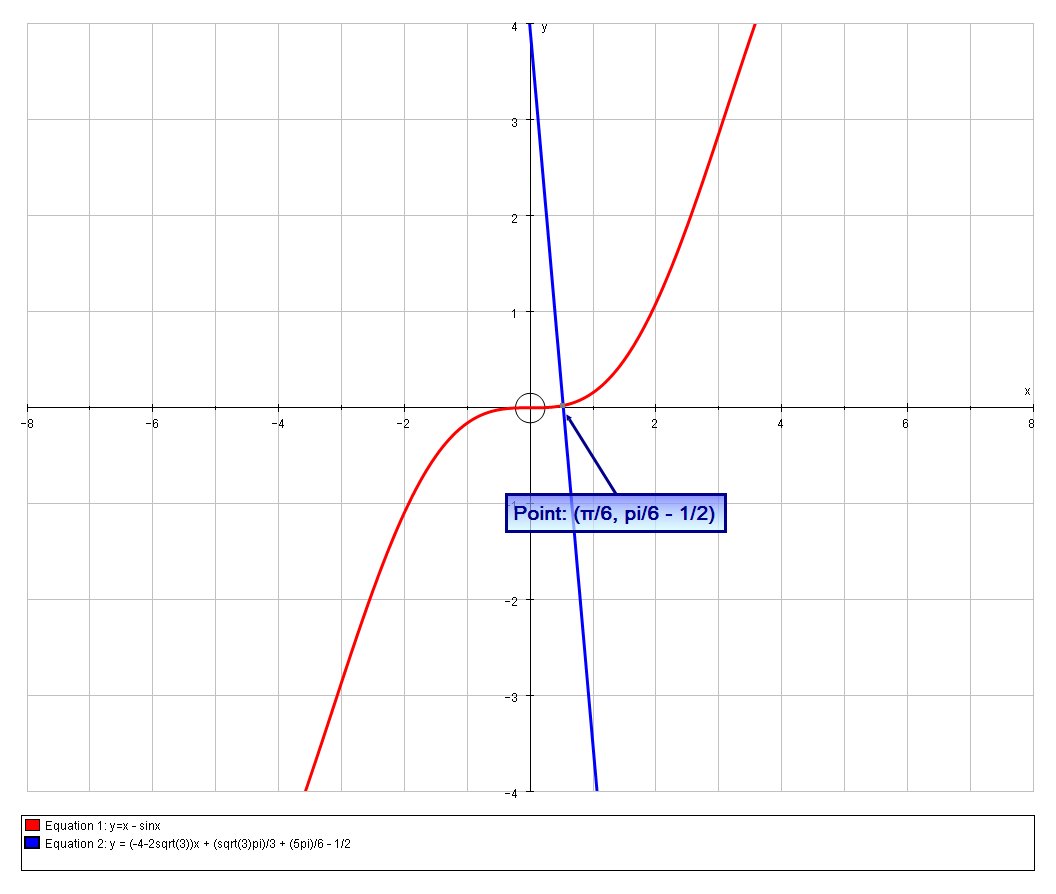
What is the equation of the normal line of #f(x)=x-sinx# at #x=pi/6#?
1 Answer
# y = (-4-2sqrt(3))x + (sqrt(3)pi)/3 + (5pi)/6 - 1/2 #
Explanation:
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. (If needed, then the normal is perpendicular to the tangent so the product of their gradients is
We have:
# f(x) = x - sinx #
Differentiating wrt
# f'(x) = 1 - cosx #
So when
# \ f(pi/6) = pi/6 - 1/2#
# f'(pi/6) = 1 - sqrt(3)/2 = (2-sqrt(3))/2#
So, the gradient of the normal is:
# m_N = -2/(2 - sqrt(3)) #
# \ \ \ \ \ \ = -2/(2 - sqrt(3)) (2 + sqrt(3))/(2 + sqrt(3))#
# \ \ \ \ \ \ = -(2(2+sqrt(3)))/(4-3)#
# \ \ \ \ \ \ = -(4+2sqrt(3))#
So the tangent passes through
# y - (pi/6 - 1/2) = -(4+2sqrt(3))(x - pi/6) #
# :. y - pi/6 + 1/2 = -4x + (4pi)/6 -2sqrt(3)x + (2sqrt(3)pi)/6 #
# :. y = -4x -2sqrt(3)x + (sqrt(3)pi)/3 + (2pi)/3+pi/6 - 1/2 #
# :. y = (-4-2sqrt(3))x + (sqrt(3)pi)/3 + (5pi)/6 - 1/2 #
We can verify this graphically: