Question

It's a calculus problem?

Answer 1

`f` has `3` relative maxima, `2` relative minima, and `6` points of inflexion at which the tangents are not horizontal.

Explanation:

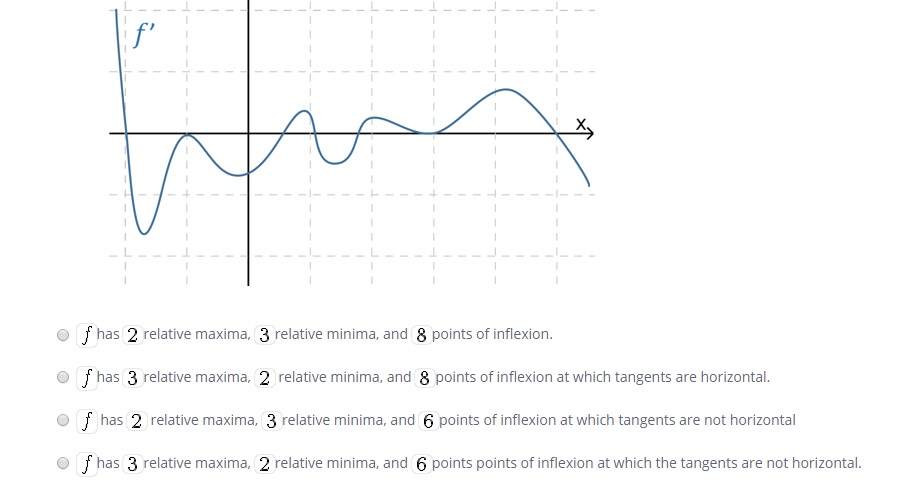
• At a local maximum, the derivative will transition from positive to negative. We see `3` examples where `f'` intersects the `x` axis, changing from positive to negative. So there are `3` local maxima.

• At a local minimum, the derivative will transition from negative to positive. We see `2` examples where `f'` intersects the `x` axis, changing from negative to positive. So there are `2` local minima.

• At a point of inflexion where the tangent is not horizontal, the derivative `f'` has a local maximum or minimum but does not touch the `x` axis. There are `6` examples of that in the given graph of `f'`.

So `f` has `3` relative maxima, `2` relative minima, and `6` points of inflexion at which the tangents are not horizontal.