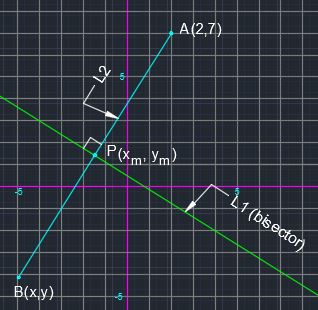
Let #L1# be the perpendicular bisector and #L2# be the bisected line, as shown in the figure.
Given that the equation of the bisector #L1# is #8y+5x=4#,
#=> y=-5/8x+1/2#
Let #m_1# be the slope of #L1#, and #m_2# the slope of #L2#,
#=> m_1=-5/8#
Recall that the product of the slopes of two perpendicular lines is #-1#,
#=> m_2xxm_1=-1, => m_2=8/5#
#=># equation of #L2# is : #y-7=8/5(x-2)#
#=> y=8/5x+(19)/5#
Set the equations of #L1 and L2# equal to each other to find the intersection point #P(x_m, y_m)#, which is also the midpoint of #L2#.
#=> -5/8x+1/2=8/5x+19/5#
#=> x=-(132)/(89)#
#=> y=-5/8x+1/2=-5/8xx(-(132)/(89))+1/2=(127)/(89)#
#=> P(x_m,y_m)=(-(132)/(89), (127)/(89))#
Let the other end point of #L2# be #B(x,y)#,
Since #P# is the midpoint of #L2#,
#=> ((x+2)/2, (y+7)/2) = (-(132)/(89), (127)/(89))#
#=> (x,y)=(-(442)/(89), -(369)/(89))#
