How to simplify logarithm?
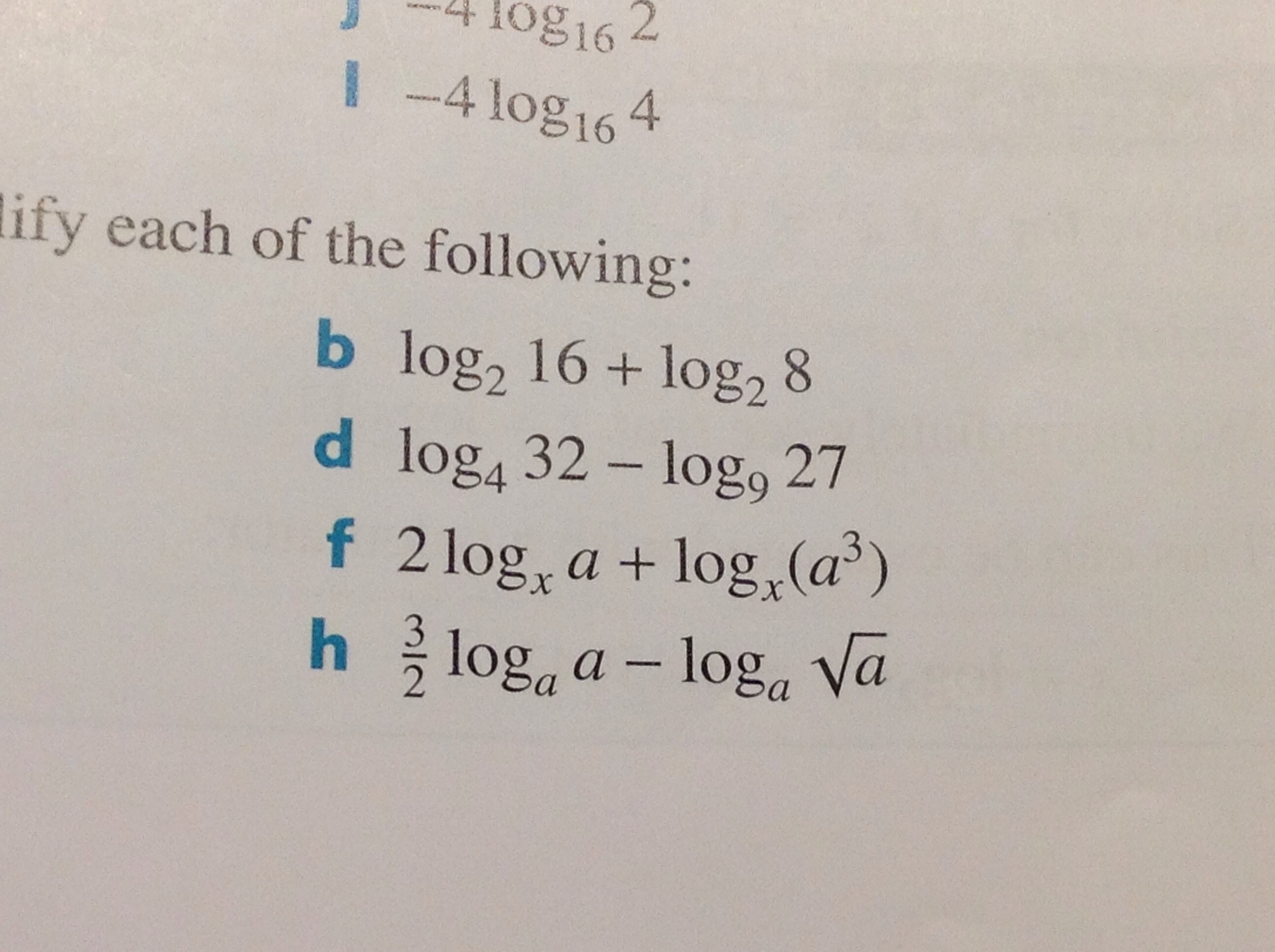
Can anyone please explain to me how to do question d, when there I see different bases? Thanks!
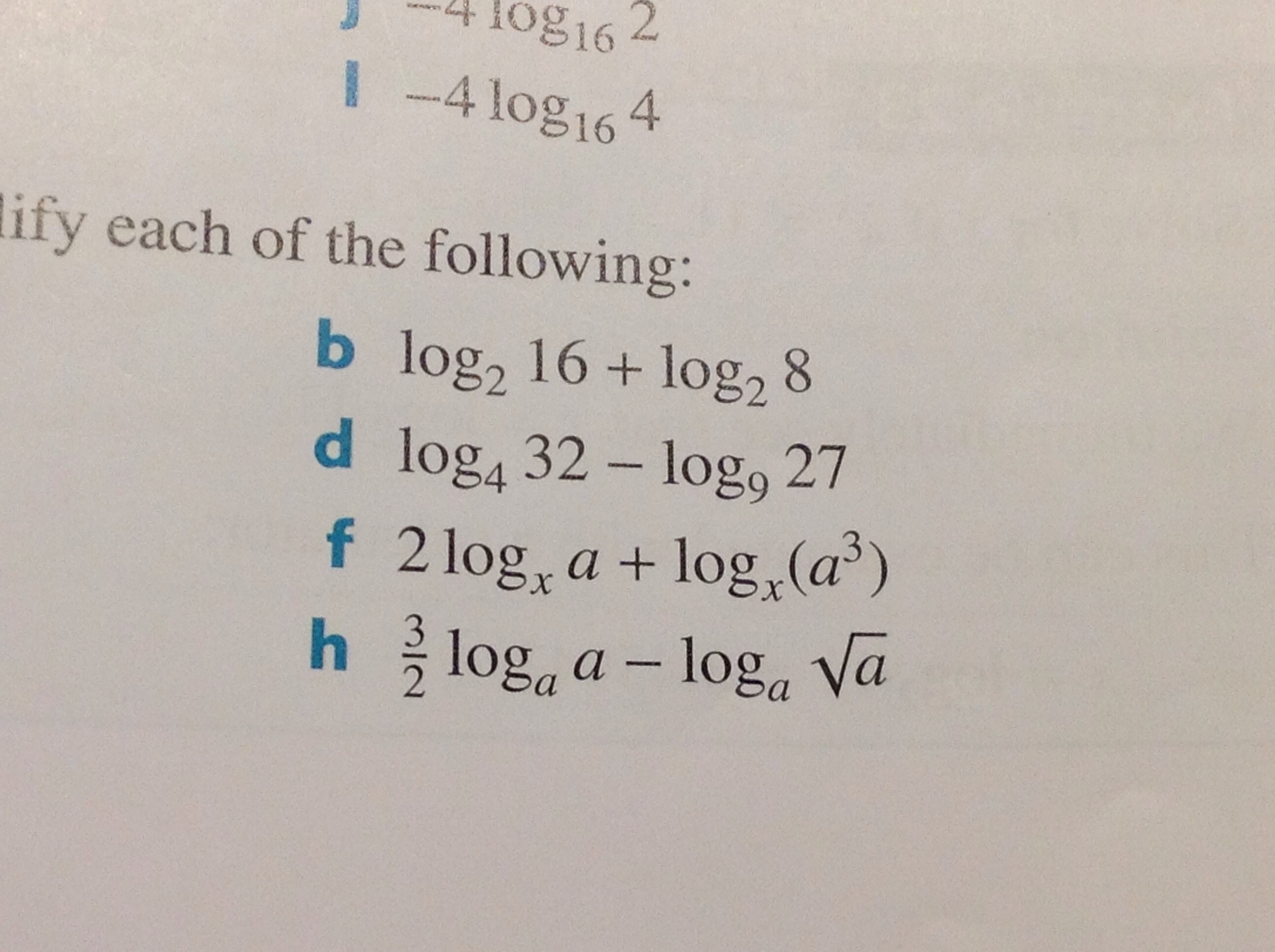
Can anyone please explain to me how to do question d, when there I see different bases? Thanks!
1 Answer
Explanation:
"there are 2 possible approaches"there are 2 possible approaches
(1)color(blue)" Evaluation"(1) Evaluation
•color(white)(x)log_b x=nhArrx=b^n∙xlogbx=n⇔x=bn
rArrlog_4 32=nrArr32=4^n⇒log432=n⇒32=4n
"express the equation in base 2"express the equation in base 2
rArr2^5=(2)^(2n)⇒25=(2)2n
"equating the exponents"equating the exponents
2n=5rArrn=5/2color(red)(larr)2n=5⇒n=52←
"similarly for "log_9 27=nsimilarly for log927=n
rArr27=9^n⇒27=9n
"expressing the equation in base 3"expressing the equation in base 3
3^3=3^(2n)33=32n
rArr2n=3rArrn=3/2color(red)(larr)⇒2n=3⇒n=32←
rArrlog_4 32-log_9 27=5/2-3/2=1⇒log432−log927=52−32=1
(2)color(blue)" Change of base"(2) Change of base
•color(white)(x)log_b a=log_c a/log_c b∙xlogba=logcalogcb
"choose base 10 as this can be evaluated on calculator"choose base 10 as this can be evaluated on calculator
rArrlog_4 32-log_9 27⇒log432−log927
=log_10 32/log_10 4-log_10 27/log_10 9=log1032log104−log1027log109
=2.5-1.5=1=2.5−1.5=1
