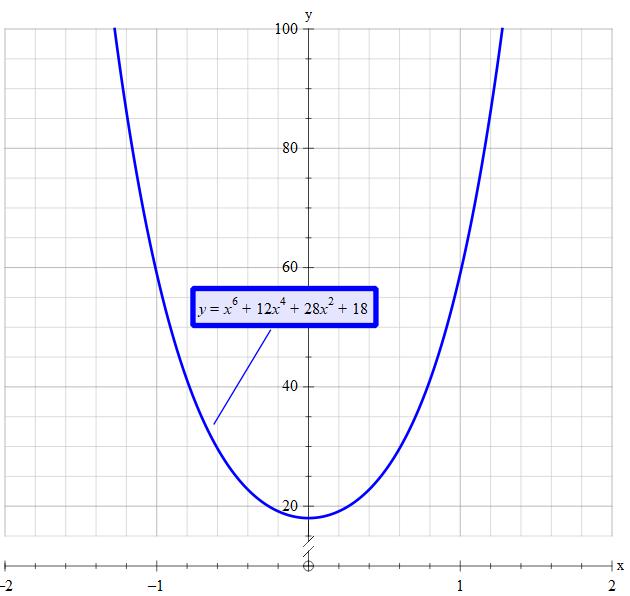
Given #x^6+12x^4+29x^2+18#
Let #t# be a substitution for #x^2color(green)(larr" Changed the wording")#
Then #t^3->(x^2)^3=x^6color(green)(larr" added explanation")#
and #t^2->(x^2)^2=x^4color(green)(larr" added explanation")#
Set #t^3+12t^2+29t+18=0#
test for #t=1#
#1+12+29+18=0 color(red)(larr"Fail")#
test for #t=-1#
#-1+12-29+18=0color(red)(larr" Works")#
One of the factors is #color(green)((t+1) ->(x^2+1)=> x=sqrt(-1))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
A cubic as at least 1 solution if equated to 0 and at most 3
Assuming three solutions.
We already have #(t+1)#
Consider the constant of 18
We have #1xx18# or #2xx9#
Consider the #12t^2# and note that #1+2+9=12# so lets run with this.
Try #t=-2#
#(-2)^3+12(-2)^2+29(-2)+18 = 0 # as required
Thus another factor is #color(green)((t+2) -> (x^2+2) => x=sqrt(-2))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Try #t=-9#
#(-9)^3+12(-9)^2+29(-9)+18=0# as required
Thus the last factor is #color(green)((t+9)->(x^2+9)=>x=sqrt(-9))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(magenta)("Check so far")#
#(t+1)(t+2)(t+9)#
#(t+1)(t^2+11t+18)#
#t^3+11t^2+18t+t^2+11t+18#
#t^3+12t^2+29t+18->x^6+12x^4+29x^2+18# as required
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(magenta)(ul("You only requested factorisation"))#
#(x^2+1)(x^2+2)(x^2+9)larr" Factorisation"#
Note that if #x!in CC# (Not complex numbers) then there is no solution to #(x^2+1)(x^2+2)(x^2+9)=0# ie no roots. That is the plot does not cross the x-axis.
However, you do decide that #x# may belongs to the set of complex numbers (#x inCC#) then we have the theoretical roots:
#[ (i)^2+1]color(white)(".")[(sqrt(2)color(white)("...")i)^2+2]color(white)(".")[(sqrt(3)color(white)("...")i)^2+9] =0#