Question

How do you calculate the left and right Riemann sum for the given function over the interval [2,14], n=6 for `f(x)= 3 - (1/2)x`?

Answer 1

`LRS = -6`
`R RS = =18`

Explanation:

We have:

`f(x) = 3-1/2x`

We want to calculate over the interval `[2,14]` with `6` strips; thus:

`Deltax = (14-2)/5 = 2`

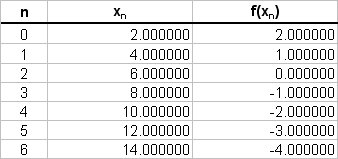
Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;

Left Riemann Sum

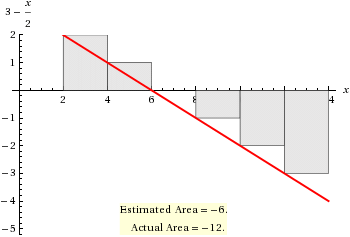
`LRS = sum_(r=0)^5 f(x_i) \ Deltax_i`
`" " = 2 * (2 + 1 - 0 - 1 - 2 - 3)`
`" " = 2 * (-3)`
`" " = -6`

Right Riemann Sum

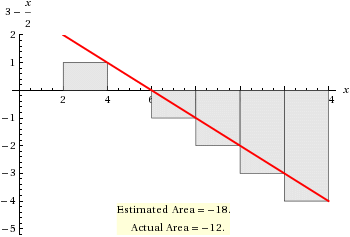
`R RS = sum_(r=1)^6 f(x_i) \ Deltax_i`
`" " = 2 * (1 - 0 - 1 - 2 - 3 - 4)`
`" " = 2 * (-9)`
`" " = -18`

Actual Value

For comparison of accuracy:

`Area = int_2^14 \ 3-1/2x \ dx`
`" " = [ 3x-x^2/4 ]_2^14`
`" " = (42-49) - (6-1)`
`" " = (-7) - (5)`
`" " = -12`

Note that as the function is linear the exact valkuye is the average of the LRS and the RRS