Prove these questions using Principle of Mathematical Induction ?
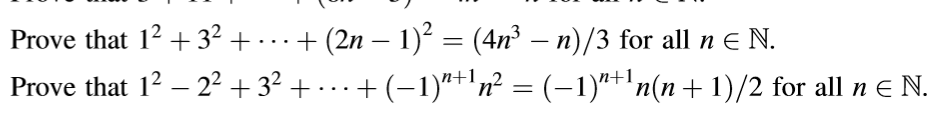
1 Answer
===========================================================
Problem 1:
=
Induction Proof - Hypothesis
We seek to prove that:
# 1^2 + 3^2 + ... + (2n-1)^2 = (4n^3-n)/3 \ \ \ \ AA n in NN #
Or, equivalently:
# sum_(r=1)^n (2r-1)^2 = (n(4n^2-1))/3 \ \ \ \ AA n in NN # ..... [A]
So let us test this assertion using Mathematical Induction:
Induction Proof - Base case:
We will show that the given result, [A], holds for
When
# LHS = 1^2 = 1#
# RHS =(4-1)/3 = 1 #
So the given result is true when
Induction Proof - General Case
Now, Let us assume that the given result [A] is true when
# 1^2 + 3^2 + ... + (2m-1)^2 = (4m^3-m)/3 # ..... [B]
Consider the LHS of [A] with the addition of the next term, in which case we have
# LHS = 1^2 + 3^2 + ... + (2m-1)^2 + (2(m+1)-1)^2 #
# \ \ \ \ \ \ \ \ = 1^2 + 3^2 + ... + (2m-1)^2 + (2m+2-1)^2 #
# \ \ \ \ \ \ \ \ = 1^2 + 3^2 + ... + (2m-1)^2 + (2m+1)^2 #
# \ \ \ \ \ \ \ \ = (4m^3-m)/3 + (2m+1)^2 \ \ \ \ # (using [B])
# \ \ \ \ \ \ \ \ = 1/3((4m^3-m) + 3(4m^2+4m+1) ) #
# \ \ \ \ \ \ \ \ = 1/3( 4m^3-m + 12m^2+12m+3 ) #
# \ \ \ \ \ \ \ \ = 1/3( 4m^3 + 12m^2+12m-m+3+1-1 ) #
# \ \ \ \ \ \ \ \ = 1/3( 4m^3 + 12m^2+12m+4-m-1 ) #
# \ \ \ \ \ \ \ \ = 1/3( 4(m^3 + 3m^2+3m+1)-(m+1) ) #
# \ \ \ \ \ \ \ \ = ( 4(m+1)^3-(m+1) )/3 #
Which is the given result [A] with
Induction Proof - Summary
So, we have shown that if the given result [A] is true for
Induction Proof - Conclusion
Then, by the process of mathematical induction the given result [A] is true for
Hence we have:
# 1^2 + 3^2 + ... + (2n-1)^2 = (4n^3-n)/3 \ \ \ \ AA n in NN # QED
===========================================================
Problem 2:
=
Induction Proof - Hypothesis
We seek to prove that:
# 1^2 -2^2+ 3^2 - ... + (-1)^(n+1)n^2 = (-1)^(n+1)(n(n+1))/2 \ \ \ \ AA n in NN #
So let us test this assertion using Mathematical Induction:
Induction Proof - Base case:
We will show that the given result, [A], holds for
When
# LHS = 1^2 = 1#
# RHS =(-1)^2(1)(2)/2 = 1 #
So the given result is true when
Induction Proof - General Case
Now, Let us assume that the given result [A] is true when
# 1^2 -2^2+ 3^2 - ... + (-1)^(m+1)m^2 = (-1)^(m+1)(m(m+1))/2 # ..... [B]
Consider the LHS of [A] with the addition of the next term, in which case we have
# LHS = 1^2 -2^2+ 3^2 - ... + (-1)^(m+1)m^2 + (-1)^((m+1)+1)(m+1)^2 #
# \ \ \ \ \ \ \ \ = (-1)^(m+1)(m(m+1))/2 + (-1)^(m+2)(m+1)^2 # using [B]
# \ \ \ \ \ \ \ \ = (-1)^(m+1)(m+1)/2 { m - 2(m+1)} #
# \ \ \ \ \ \ \ \ = (-1)^(m+1)(m+1)/2 { (-1)(2(m+1)-m) } #
# \ \ \ \ \ \ \ \ = (-1)^(m+2)(m+1)/2 { 2m+2-m } #
# \ \ \ \ \ \ \ \ = (-1)^(m+2)(m+1)/2 { m+2 } #
# \ \ \ \ \ \ \ \ = (-1)^(m+2) ( (m+1) { (m+1)+1 } )/2 #
Which is the given result [A] with
Induction Proof - Summary
So, we have shown that if the given result [A] is true for
Induction Proof - Conclusion
Then, by the process of mathematical induction the given result [A] is true for
Hence we have:
# 1^2 -2^2+ 3^2 - ... + (-1)^(n+1)n^2 = (-1)^(n+1)(n(n+1))/2 \ \ \ \ AA n in NN # QED

