If a liquid from a completely filled spherical container of inner radius r is poured into a cube shaped container, what would be the dimensions of the cube in terms of the radius of the sphere?
1 Answer
Sep 28, 2017
Explanation:
Volume of cube is equal to volume of sphere.
Volume of a sphere:
Let
Then:
So we have:
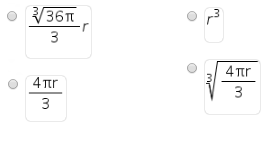
Volume of cube = volume of sphere:
We need to manipulate
Since
This then gives:
Now we have:
Taking cube roots:
Extracting and evaluating any cubes:
Which can be expressed:

