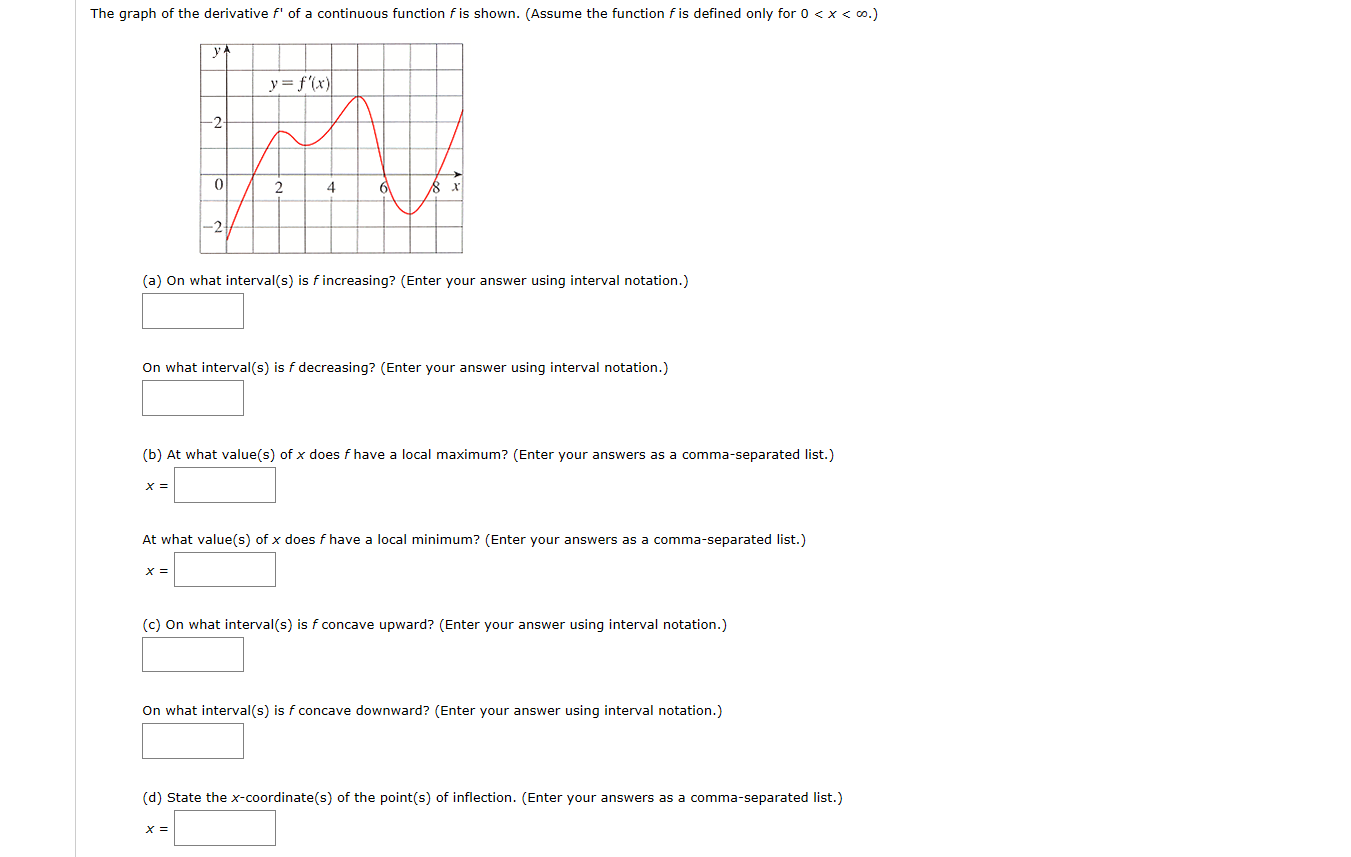
Recall that the derivative #f'(x)# measures the rate of change of that function with respect to the given variable. Thus, if for some #x_0, f'(x_0)=k#, that means that at #x=x_0#, the function is changing at a rate of #k# units for every one unit on the x-axis. If #f'(x)>0#, the function is increasing at that point; #f'(x)<0# means it is decreasing, and #f'(x)=0# means that it is neither increasing nor decreasing.
This in mind, we see that #f'(x)>0# for #1 < x < 6# and #x>8#, and #f'(x) < 0# for #0 < x<1# and #6 < x <8#. Therefore, the answer to part 1 of (a) is #(1,6) & (8,oo)#; the answer to the second part is #(0,1) & (6,8)#
For part c, the function is concave upwards when #f'(x)# is increasing, and downwards when decreasing. This would in many cases be most easily observed by graphing #f''(x)# the same way that #f'(x)# is already graphed, and declaring the original function concave upward for #f''(x)>0# or concave downward for #f''(x)<0#. However, looking at the graph is only slightly more intensive.
Examining the graph, we see that #f'(x)# is increasing on #(0,2), (3,5), & (7,oo)#, and decreasing on #(2,3) & (5,7)#. The first set of intervals will answer part 1 of c, and the second will answer part 2 of c.
Inflection points occur where the function changes concavity; more generally, inflection points occur when #f''(x)# changes sign. Since a function is concave upward for #f''(x)>0# and downward for #f''(x)<0#, all we need to do is find the points where concavity changes. From our answers to c, we can tell that these will be #x= 2,3,5,7#