First, write the integral as a sum:
int_{-3}^{1}(1+sqrt(9-x^2))dx=int_{-3}^{1}1dx+int_{-3}^{1}sqrt(9-x^2)dx.
The area under the graph of y=1 for -3<=x<=1 is the area of a rectangle: base * height=4*1=4. Hence, int_{-3}^{1}1dx=4.
Next, write int_{-3}^{1}sqrt(9-x^2)dx=int_{-3}^{0}sqrt(9-x^2)dx+int_{0}^{1}sqrt(9-x^2)dx.
The graph of y=sqrt(9-x^2) is a semicircle of radius 3 centered at the origin. For -3<=x<=0, we get a quarter circle of area 1/4 pi*3^2=(9pi)/4.
Hence, int_{-3}^{0}sqrt(9-x^2)dx=(9pi)/4.
The remaining region to calculate the area is the area under the graph of y=sqrt(9-x^2) for 0<=x<=1. This region can be split into a triangle and a sector of the circle. See the figure below.
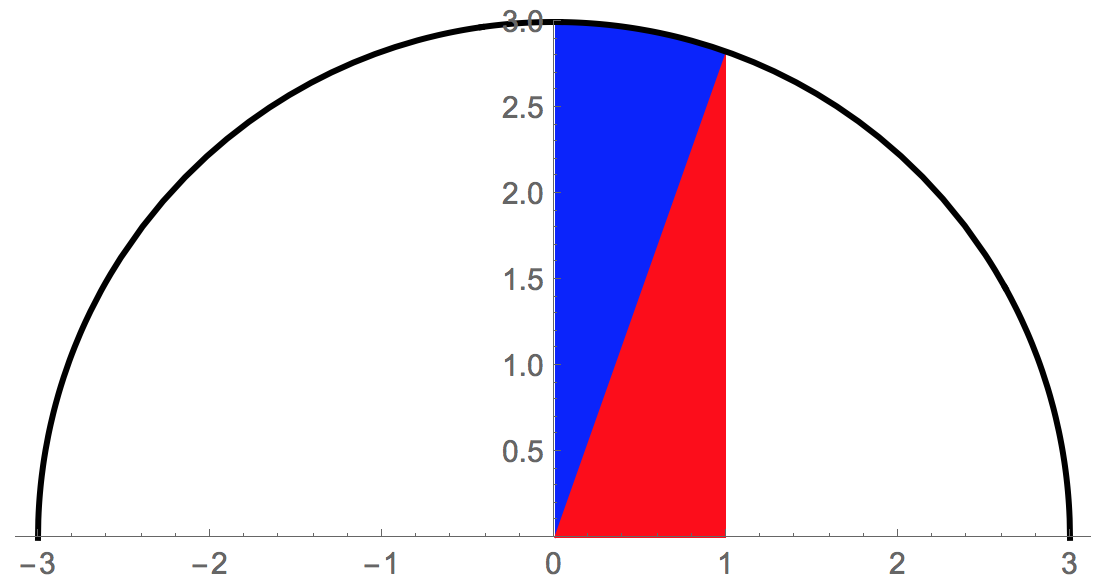
The triangle has base=1 and height=sqrt(9-1^2)=sqrt(8)=2sqrt(2). Therefore, its area is 1/2 * 1 * 2sqrt(2)=sqrt(2).
The angle for the sector of the circle is congruent to the upper angle for the triangle, which can be written as theta=arcsin(1/3) since the hypotenuse of the triangle has length 3. The area of the sector is therefore 1/2*r^2*theta=1/2*3^2*arcsin(1/3)=9/2 arcsin(1/3).
Therefore, int_{0}^{1}sqrt(9-x^2)dx=sqrt(2)+9/2 arcsin(1/3).
Putting these things all together gives the final answer of 4+sqrt(2)+(9pi)/4+9/2 arcsin(1/3) approx 14.0121


