'Find the equation of the tangent to the curve ay^2=x^3 at the point (at^2,at^3) where a>0 and t is a parameter ?
1 Answer
# y = 3/2tx - 1/2at^3 #
Explanation:
We have a family of curves defined for
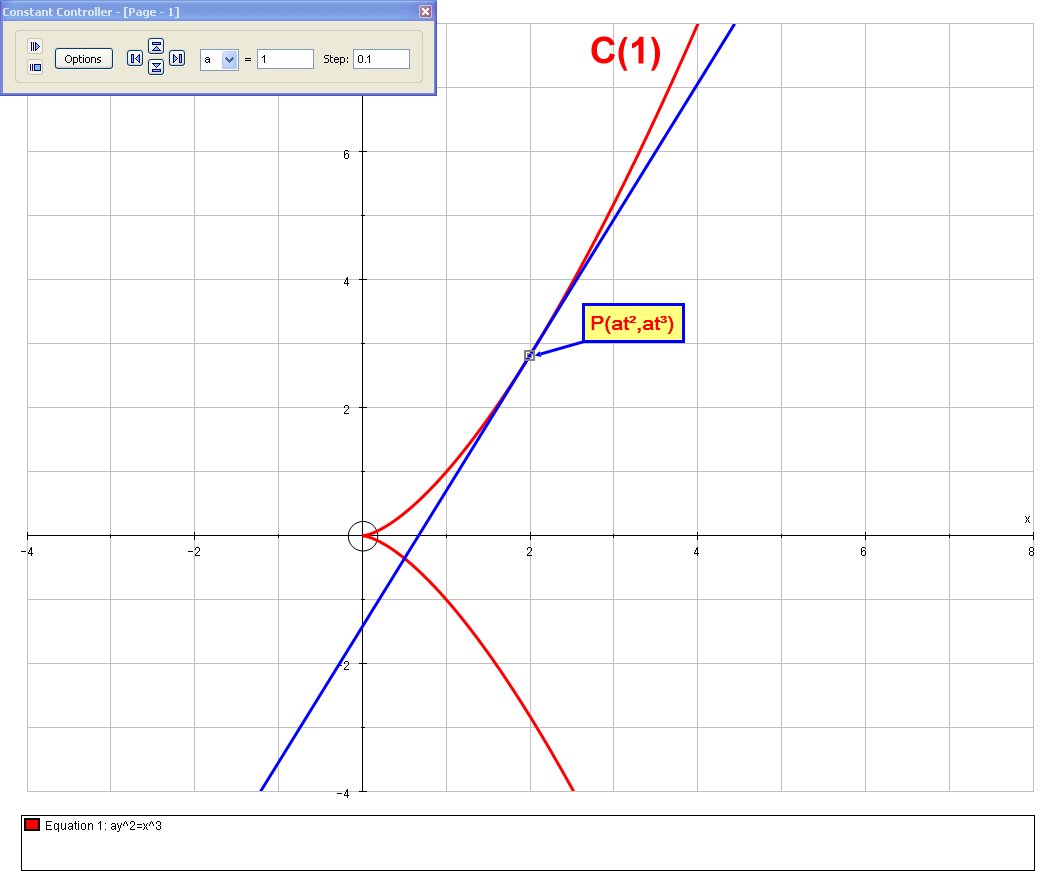
# C(a) : " " ay^2 = x^3 # ..... [A]
Or in parametric form:
# C(a) : " " { (x(t)=at^2), (y(t)=at^3) :} #
Here we have a plot for
If we differentiate equation [A] implicitly wrt
# 2ay dy/dx = 3x^2 => dy/dx = (3x^2)/(2ay) #
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. So, at a generic point
# m_T = (3x^2)/(2ay) = (3(at^2)^2)/(2a(at^3)) = (3a^2t^4)/(2a^2t^3) = 3/2t#
So the tangent passes through
# y - at^3 = 3/2t( x - at^2 ) #
# :. y - at^3 = 3/2tx - 3/2at^3 #
# :. y = 3/2tx - 1/2at^3 #
Which is the sought equation.