Consider the following picture of the situation, with the point #R# as the rocket and the point #B# as the boy.
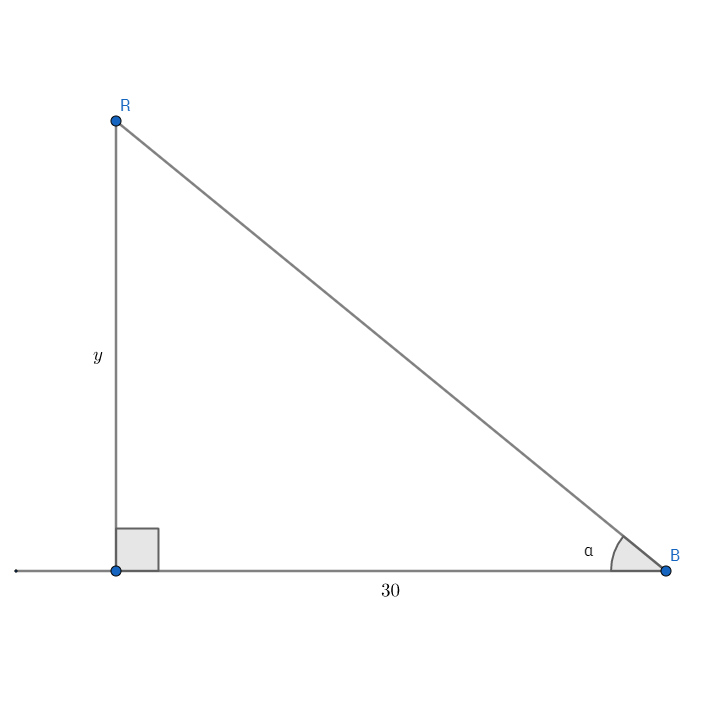
We have to make some assumptions here to solve the problem, but they are generally "safe" for this type of word problem. First, we assume the rocket is traveling perfectly vertical in its flight. (In other words, the angle formed by the rocket path with the ground is #90^o#.) Also, we assume that we are measuring the elevation angle of the rocket from the ground and not from the boy's eyes, which would be some measure above the ground, thus reducing the "net" height #y# of the rocket in the image above.
The elevation angle is described by the angle #alpha# in the image above. To determine the rate of change of the elevation angle, we need an expression for #alpha# that we can differentiate with respect to time #t#. One possible expression for #alpha#, using the diagram, is as follows:
#tan alpha = y/30#
If we take the derivatives of both sides with respect to #t#:
#d/(dt) (tan alpha) = d/(dt) (y/30)#
#sec^2 alpha * (d alpha)/(dt) = 1/30 * (dy)/(dt)#
# (d alpha)/(dt) = 1/30 * (dy)/(dt) * cos^2 alpha #
However, we are given the rate of change of the rocket height #y# as "3 meters per second", so #(dy)/(dt) = 3#. (Note this is positive because the height #y# is increasing over time.)
The one element we are missing in the expression for #(d alpha)/(dt)# above is the angle #alpha#. Without that, we cannot evaluate #cos^2 alpha#, can we?
There's two ways to go about this from this point. One is clever if the reader is observant. The other will work for certain, but takes some more effort to reach the same conclusion. We know from the problem that the moment being discussed has the rocket 30 meters above the ground. Knowing this, along with the Pythagorean Formula allows us to calculate the hypotenuse:
#c^2 = y^2 + 30^2 = 30^2 + 30^2 = 1800#
#c = 30sqrt(2)#
We can now proceed:
# (d alpha)/(dt) = 1/30 * (3) * (30/(30sqrt(2)))^2 = 1/20 "radians"//s#
By the way, the clever part was to recognize that the height #y# matched the base of 30 meters, making this a 45-45-90 right triangle, meaning you could skip straight to #cos (pi/4) = 1/sqrt(2)# immediately.

