Given that #log(2) ~~ 0.3010#, what is #log(0.005)# ?

Question

2536 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-10-07T14:49:42

I got: #-2.3# (but probably there is a faster and easier way to solve it....)

We can write:
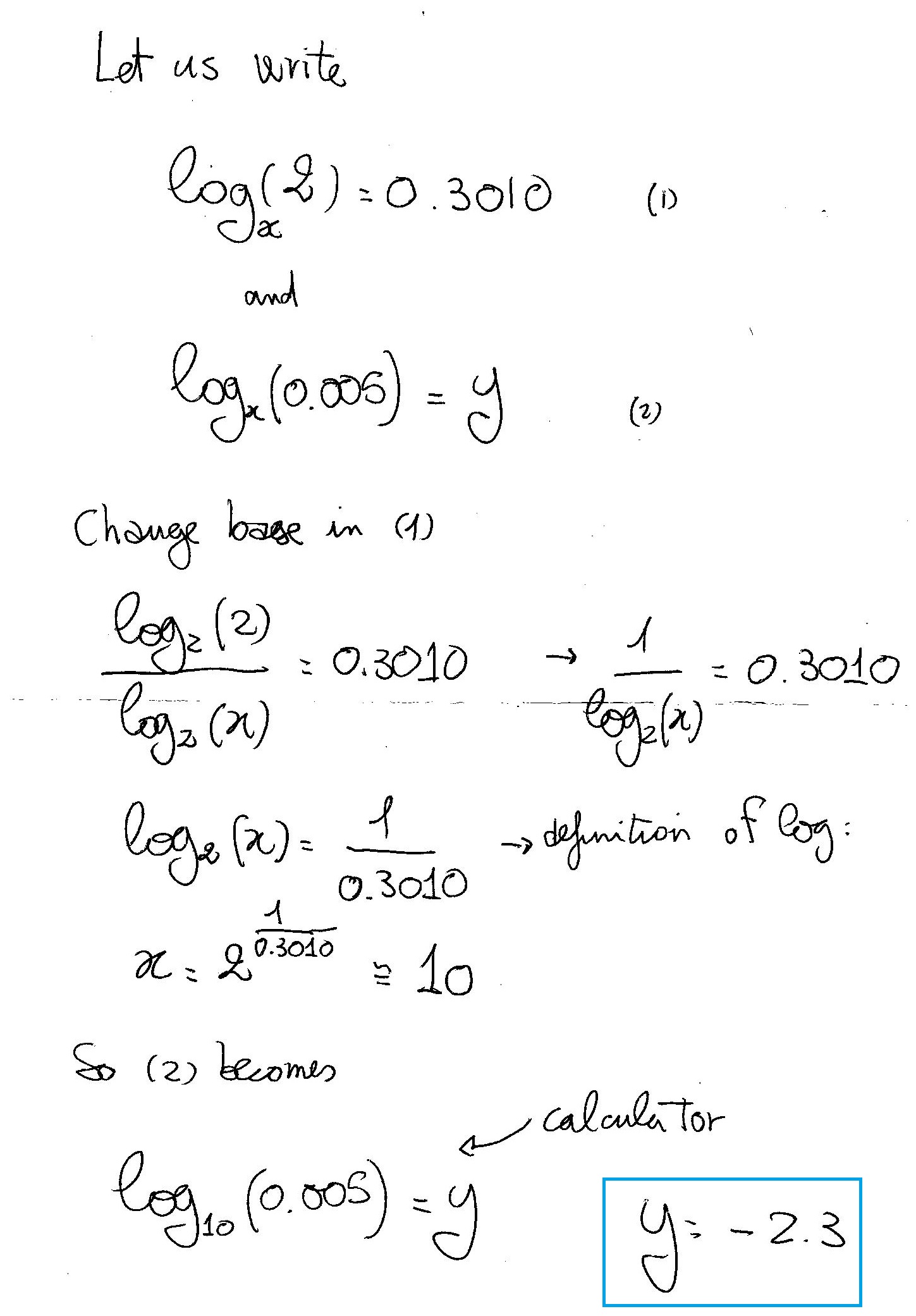
enter image source here

Answer 2 · 2017-10-12T22:00:43

#log(0.005) ~~ -2.3010#

#log(0.005) = log(1/200) = log(1)-log(200) = -log(2)-log(100) ~~ -0.3010-2 = -2.3010#

Note

I am surprised that the approximation #log(2) ~~ 0.3010# is used, since the approximation #log(2) ~~ 0.30103# is so good.

Note that #log(2) ~~ 0.301029995664#. So remembering #log(2) ~~ 0.30103# gets you a lot of accuracy for a little memory.